[AI数理]徹底的に交差エントロピー(2)

おはようございます！(株) Qualiteg 研究部です。

早速、前回の続きをやっていきましょう！

2章 分類問題は「確率」の予測として解釈する

Deep Learning やロジスティック回帰などで解きたい 分類問題 では、入力データがどのクラスに分類されるのかを予測します。

まず入力データが 何かに 分類される とはどういうことなのかを考えてみます。

たとえば、ある動物の画像を入力データとしたとき、その画像がイヌ、キツネ、オオカミ の3つのうちどれなのかを予測する 分類器 を考えます。

（分類器 は 入力と処理と出力があり、入力は画像データで、処理として ニューラルネットワーク や ロジスティック回帰 などの 計算処理 をおこない、分類結果を出力するプログラムコードと考えます）

この 分類器 にたとえば　「イヌ」の画像を入力し、分類させた結果は 「イヌ」 とダイレクトに判定されるわけではありません。

ではどのように 分類するか というと、以下のように「イヌ」である確率 0.8、「キツネ」である確率は 0.1 、「オオカミ」である確率は 0.1 のように、確率値の予測という形をとります。

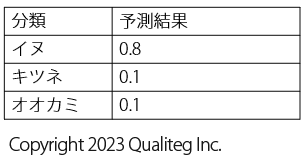
このように 分類問題が確率値の予測 であることをまず念頭において、これから交差エントロピーをみていきます。

3章 サイコロの出目（でめ）と尤度関数

さて、さきほど 分類問題は確率値の予測 とかいたとおり、ここからは、確率の考え方をつかって交差エントロピーを導き出していきたいとおもいます。

ここにサイコロがあります。

ただのサイコロではなく、どうも何か特別な細工がされているサイコロです。

つまりイカサマサイコロなので、出る目に偏りがあるという設定です。

3-1. 事象

ここで、サイコロ振ったときに起こる 事象 について考えます。事象というのは　起こった事柄　です。サイコロを振ったときに起こる事象というのは、つまるところ、　何かの目がでる　ということになります。

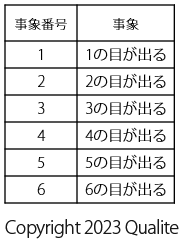
サイコロなので、サイコロを振ったときに起こりうる事象は以下の６つになります。

以降、この 6 つの事象に番号をつけて 「事象 \(_1\) 」、「事象 \(_2\) 」、「事象 \(_3\) 」のように呼ぶことにします。

3-2. ある目がでる確率

ここからは、実際にサイコロを投げて、出目を集計して「どの目が、どのくらいの確率で出るか 」を推定する方法を考えていきたいと思います。

公正なサイコロなら、どの目も \(\frac{1}{6}\) の確率で出ますが、前述のとおり、今回の設定は　細工されたイカサマサイコロなので、どの目がどのくらいの確率で出るのかは事前には予測できない設定です

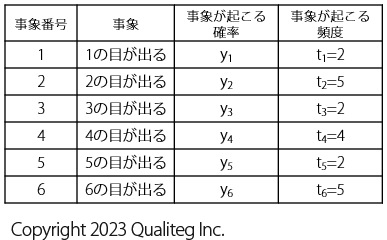
ということで、知りたいのは、このサイコロの各目（め）がでる確率なので、以下のように表に 事象が起こる確率 を追加します。

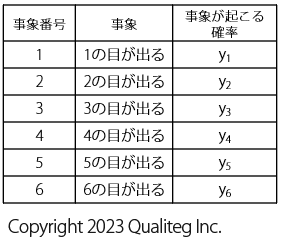
１の目が出る確率は \(y1\) 、２の目が出る確率は \(y2\) といった具合に変数 \(y1\) ～ \(y6\) として設定しました。

サイコロを投げると \(1\) ～ \(6\) のどれかの目がでるので、 事象が起こる確率 ＝　何らかの目がでる確率　の合計値は当然 \(1\) になります。

$$
y_{1} + y_{2} + y_{3} + y_{4} + y_{5} + y_{6} = 1 \tag{3.1}
$$

\(\sum\) をつかって書き直す以下のようになりますね。

$$
L = \sum_{i=1}^{6} y_i = 1 \tag{3.2}
$$

3-3. 実際にサイコロを投げる

さて、サイコロを投げて、出た目がどうなるか見ていきます

このサイコロを２０回投げた結果が以下のようになっていたとします。

（ぱっと見、どうも偶数の目が多く出やすいサイコロのようです）

２０回投げた結果、１の目が２回、２の目が５回　というように、各事象がどのくらいの頻度で発生したかどうかがわかったので、さきほどの表に 事象が起こる頻度 という列を加え以下のようにしました。

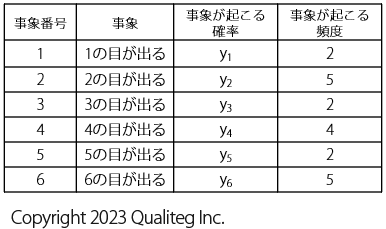
3-4. 尤度（ゆうど）関数

さて、今まで整理した結果をつかって確率を計算していきます。

さきほどの表で 事象が起こる頻度 を \(t\) という変数におきかえて、事象番号の添え字 を付与して \(t_{1}\) ～ \(t_{6}\) であらわすと以下のようになります。

サイコロを２０回投げて上の表のようになる確率はどうなるでしょう？

サイコロを投げるという試行は独立（２投目の結果は１投目の影響を受けない）なので、1の目が2回、2の目が5回、3の目が2回、4の目が4回、5の目が2回、6の目が5回出たのでその確率を計算すると

$$
y_{1} \times y_{1} \times y_{2} \times y_{2} \times y_{2} \times y_{2} \times y_{2} \times y_{3} \times y_{3} \times y_{4} \times y_{4} \times y_{4} \times y_{4} \times y_{5} \times y_{5} \times y_{6} \times y_{6} \times y_{6} \times y_{6} \times y_{6}
$$

となります。

これを事象が起こる頻度を \(t_{1}\) ～ \(t_{6}\) を指数として使ってべき乗表記に書き直すと

$$
y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}} \cdot y_{4}^{t_{4}} \cdot y_{5}^{t_{5}} \cdot y_{6}^{t_{6}}
$$

となります。
(ついでに \(\times\) も \(\cdot\) に置き換えました)

この　サイコロを投げた時の 事象 \(1\) ～ 事象 \(6\) が起こる確率 \(y_{1}\) ～ \(y_{6}\) を式に含む \(y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}} \cdot y_{4}^{t_{4}} \cdot y_{5}^{t_{5}} \cdot y_{6}^{t_{6}}\) を尤度（ゆうど）関数（または単に尤度）と呼びます。

「尤度」は英語の likelihood に相当する単語なので、 \(L\) をつかって　尤度関数は以下のようになります

$$
L = y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}} \cdot y_{4}^{t_{4}} \cdot y_{5}^{t_{5}} \cdot y_{6}^{t_{6}}　\tag{3.3}
$$

\(y\) の添え字となっている事象番号を \(i\) であらわし、積を 総乗の記号 \(\prod\) であらわすと、以下のようになります

(\(\prod\) は \(\sum\) のかけ算版です）

$$
L = \prod_{k=1}^{6} y_k^{t_{k}} \tag{3.4}
$$

ここでお題をもう一度思い出します。

「今回のイカサマサイコロは出目に偏りがあるので、どの目が、どのくらいの確率で出るか を推定する方法」を考えたい　ということでした。

この方法の１つに　最尤推定 (最尤法) 　があります。

最尤推定の問題設定は 「今回の20回の試行の結果をよく説明する良さげな \(y_{1}\) ～ \(y_{6}\) は何か」 となります。

これを言い換えると、
「 \(y_{1}\) ～ \(y_{6}\) の値が何ならば、今回の20回の試行の結果のようになるか」 となります。

これはつまり、さきほどの尤度関数 \(L\) を最大にするような 確からしいパラメータ \({y_{1}}\) , \({y_{2}}\) , \({y_{3}}\) , \({y_{4}}\) , \({y_{5}}\) , \({y_{6}}\) を求めることになります。

3-5. 最尤推定

これまでの流れで、「尤度関数 \(L\) を最大にするパラメータ \({y_{1}}\) , \({y_{2}}\) , \({y_{3}}\) , \({y_{4}}\) , \({y_{5}}\) , \({y_{6}}\) 　を求める」、という問題設定となりましたが、尤度関数 \(L\) を最大化するにはどうしたらよいでしょうか。

ある関数の最大値を求める方法として、その関数を微分し、その値が \(0\) となる場所を求める方法があります。

ある関数を微分すると微分した後の関数（＝導関数）は元の関数の接線の傾きをあらわしますので、その傾きが \(0\) となるような点が元の関数が最大値をとる場所となります。

（より正確にいうと、接線の傾きが \(0\) になる点は元の関数の極大値または極小値をとることになりますが尤度関数の2階微分（2次微分ともいう。関数を2回微分すること)を調べることで傾きが \(0\) になる点＝極大になる、ことを補足で説明します）

このように、尤度関数 \(L\) を最大にするパラメータ（＝最尤推定値）を求めることを　最尤推定（最尤法） とよびます。

3-6. 対数尤度関数

尤度関数の最大値を求めるには、その微分値が \(0\) となる点を求めることですので、尤度関数 \(L\) を微分したいとおもいますが、尤度関数は以下の通り　かけ算　の形式となっており、このままだと微分がやりづらいという問題と、後からコンピュータで計算するときに、確率値( \(0\) ～ \(1\) )の積算をえんえんとやることになるため、その計算値が極めて小さくなりコンピュータの数値演算精度を考えると問題になる可能性があります。

そこで、尤度関数 \(L\) に以下のように 対数 をとった、 対数尤度関数 \(log L\) を考えます。

対数 \(log\) をとると、 かけ算を足し算 にする効果があるので、微分や計算がやりやすくなります。

さっき \(\prod\) を使って書いた 尤度関数 \(L\) をもう１度、展開し、

$$
\begin{aligned}
L &= \prod_{k=1}^{6} y_k^{t_{k}}& \
&= y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}} \cdot y_{4}^{t_{4}} \cdot y_{5}^{t_{5}} \cdot y_{6}^{t_{6}}&
\end{aligned}
$$

以下のように尤度関数に対数をとった \(log L\) のカタチにします。
尤度関数に対数をとってるので 対数尤度関数 と呼びます。

$$
\log L = \log (y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}} \cdot y_{4}^{t_{4}} \cdot y_{5}^{t_{5}} \cdot y_{6}^{t_{6}}) \tag{3.5}
$$

対数の公式

ここで、ちょっと対数の公式を思い出しておきましょう

対数の公式①

$$
\log ab = \log a + \log b
$$

対数の公式②

$$
\log a^{b} = b \log a
$$

対数の公式を思い出したところで、式 (\(3.5\)) を変形していきます

$$
\begin{aligned}
\log L =&\log (y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}} \cdot y_{4}^{t_{4}} \cdot y_{5}^{t_{5}} \cdot y_{6}^{t_{6}})& \
\
&対数の公式①より、 \log のかけ算をたし算に変形&\\
=&\log y_{1}^{t_{1}} + \log y_{2}^{t_{2}} + \log y_{3}^{t_{3}} + \log y_{4}^{t_{4}} + \log y_{5}^{t_{5}} + \log y_{6}^{t_{6}}&\
\\
&対数の公式②より、肩にある指数をおろす&\\
=&t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3} + t_{4} \log y_{4} + t_{5} \log y_{5} + t_{6} \log y_{6} &\
\
\end{aligned}
$$

対数をとることにより、このように取り扱いやすいカタチとなりました。

$$
\begin{aligned}
\log L=&t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3} + t_{4} \log y_{4} + t_{5} \log y_{5} + t_{6} \log y_{6} &
\end{aligned}
$$

さらに、添え字 \(1\) ～ \(6\) を \(k\) に置き換えて \(\sum\) であらわすと、以下のようになります。

$$
\log L=\sum_{k=1}^{6} t_{k} \log y_{k} \tag{3.6}
$$

ここまでで、サイコロを20回投げた出目の対数尤度関数は以下のようになりました

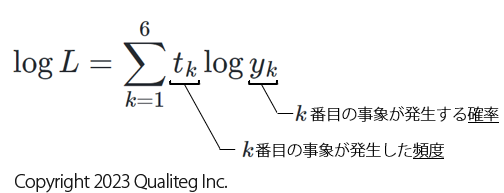
ところで、20回なげた20回という試行回数はどこに行ってしまったんだということになりますが、これは 頻度 \(t_{k}\)　の合計値、すなわち \(\sum_{k=1}^{6}t_{k}\) に反映されています。

$$
\sum_{k=1}^{6}t_{k} = 20
$$

まとめ

いかがだったでしょうか。

今回は、分類問題を確率の視点から捉えるという考え方を基に、サイコロの出目を推定するという具体的な確率問題について学んでいきました。普通のサイコロではすべての目が等しい確率で出ますが、今回は特殊な例として、ある目が出やすいように偏りがあるサイコロを使ってみました。

このような偏ったサイコロを振ったときに、どの目がどれくらいの頻度で出るかを、変数を用いて表す「尤度関数」を作成し、これをを用いて、各目が出る確率をどのように推定するかを考えるために、「最尤推定」という手法をご紹介しました。

さらに、この推定方法をもっと扱いやすくするために、尤度関数に対数を取った「対数尤度関数」を導入し、数学的に（そしてコンピュータに計算しやすい）シンプルで分かりやすい形にする工夫をしました。

このプロセスを通じて、偏りのあるサイコロの振り方から、実際にどのように確率を計算するかの具体的な手順を見てきました。

次回は、尤度関数から交差エントロピーを導いていってみたいとおもいます。

それでは、また次回お会いしましょう！

参考文献
https://blog.qualiteg.com/books/

navigation