[AI数理]徹底的に交差エントロピー(3)
![[AI数理]徹底的に交差エントロピー(3)](/content/images/size/w1200/2024/04/ce03.png)
おはようございます!(株) Qualiteg 研究部です。
今回は、尤度関数から交差エントロピーを導いていきたいとおもいます!
4章 尤度関数から交差エントロピーを導く
さて、今までは 20回ぶんサイコロを投げて、起こった事象(出た目が1なのか、2なのか、・・・、6なのか) を数えた結果を以下の表のようにまとめました。
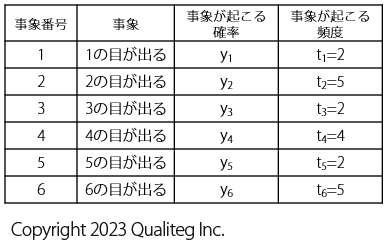
では、こんどは、1回ぶんサイコロを投げたときどうのようになるかみてみます。
1回サイコロをなげた結果が 1の目 だった場合は、以下のように書くことができます。
(でた目のところに✔マークをいれただけです)
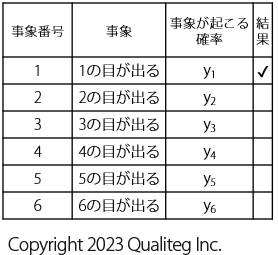
さて、?だと計算にもっていきづらいので、出た目のところを \(1\) にして、出なかった目は \(0\) と置き換えることにします。
( \(1\) が記載されている目は その目にとっては 頻度 = 確率 = \(1\) と考え、 \(0\) が記載されている目は、その試行では出なかったので、 頻度 = 確率 = \(0\) と考えると理解しやすいかもしれません。)
すると、結果 列は以下のように \(1\) と \(0\) であらわすことができます。
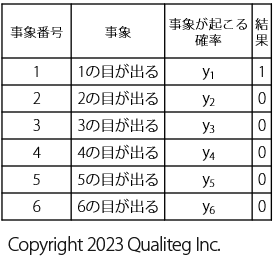
さらに、さきほどまでの表にも書いていたように 結果 列を、ふたたび、 事象が起こる頻度 として \(t\) で表現すると、以下のようになります。
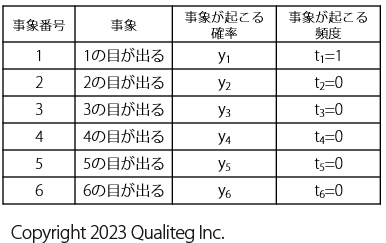
これを再度、対数尤度関数の式で表記すると
$$
\log L=\sum_{k=1}^{6} t_{k} \log y_{k} \tag{4.1}
$$
はい、この 式 \((4.1)\) これは 式 \((3.6)\) とまったく同じです。ただし、裏にある設定は、 1回だけの試行についての対数尤度関数(※) のように解釈できる点が 式 \((3.6)\) と異なる点です。
※1回だけの試行についての対数尤度関数 というと、かえってやっかいですが、よくかんがえてみると、尤度というのはそもそも複数の確率の積になっているため、1回の試行についてのだけに着目したときの対数尤度関数は 尤度 というよりも 指数つきで表現された確率に対数をとっただけのもので実質、ただの 確率 です。では、なぜこのようなまどろっこしい解釈をわざわざするかというと、後半にでてくる 交差エントロピー の式への呼び水とするためです。
では、「1の目が出る」という事象が起こった 1回だけの試行について、 式 \((3.7)\) を実際に計算してみましょう。
$$
\begin{aligned}
\log L= &t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3} + t_{4} \log y_{4} + t_{5} \log y_{5} + t_{6} \log y_{6} &
\
= &1 \cdot \log y_{1} + 0 \cdot \log y_{2} + 0 \cdot \log y_{3} + 0 \cdot \log y_{4} + 0 \cdot \log y_{5} + 0 \cdot \log y_{6}
\end{aligned}
$$
頻度 \(t\) は 1つだけ \(1\) で、あとは \(0\) になるので、このようにシンプルな計算となりますね。
今回はサイコロだったので 6個の事象 が対象でしたが、これを \(K\) 個の事象というふうに一般化すると
$$
\log L=\sum_{k=1}^{K} t_{k} \log y_{k} \tag{4.2}
$$
のように書くことができます。
この式 \((4.2)\) は 1件あたりの対数尤度関数、もうすこし統計学的な言い方をすれば 1つの標本データ あたりの 対数尤度関数 となります。
対数尤度関数は大きくなるほど、確からしいパラメータ \(y_{k}\) を持つことになりますが、 Deep Learning 等の機械学習では損失関数が 小さくなるように 学習させていきますので、式 \((4.2)\) にマイナスをつけた式 \((4.3)\) のことを 交差エントロピー関数 と呼びます。
交差エントロピー関数(標本データ1件ぶんバージョン)
$$
\ - \log L=\sum_{k=1}^{K} t_{k} \log y_{k} \tag{4.3}
$$
これで交差エントロピー関数を導くことができました。
めでたしめでたし👏
え? ちがう?
伏線の回収忘れ?
「サイコロの各目の確率 \(y\) の話はどうなった?」
「対数尤度関数の導関数が \(0\) になる点をみつけて、サイコロの各目がでる確率求めないの?]
「対数尤度関数の微分して \(0\) になった点は極大または極小であって、最大ではないでしょう?」
「いやいや、待て、尤度関数に対数つけたのは、微分しやすくなるからでしょう。対数尤度関数は微分しないわけ?」
はい、おっしゃるとおりですね、この点については、「補足」にて別途説明いたします。
といいますのも、サイコロの各目がでる確率は最尤推定の手法にて求められますが、本シリーズは「交差エントロピー関数」を導き出す部分が主眼なので、「交差エントロピー」がうっすら見えてきた今、サイコロの目の確率推定トピックは少しあとまわしにさせていただき、もうすこし交差エントロピーを掘り下げてみたいとおもいますので、おつきあいくださいませ!
それでは、また次回お会いしましょう!
参考文献
https://blog.qualiteg.com/books/
navigation




