[AI数理]対数関数の微分法・後編
![[AI数理]対数関数の微分法・後編](/content/images/size/w1200/2024/04/taisu_kouhen.png)
おはようございます!(株) Qualiteg 研究部です。
本日は対数関数の微分法の後編です!
今回で、対数関数の微分法をマスターしましょう!
2. 対数関数の公式
まず、対数関数の公式をおさえておきます。あとで対数関数の微分法の導出で使用します
\(a^{0} = 1\) 、つまり \(a\) を \(0\) 乗すると \(1\) となるため
$$
\log_a 1 = 0 \tag{2.1}
$$
\(a^{1} = a\) 、つまり \(a\) を \(1\) 乗すると \(a\) となるため
$$
\log_a a = 1 \tag{2.2}
$$
積の対数
$$
\log_a (X \times Y) = \log_a X + \log_a Y \tag{2.3}
$$
商の対数
$$
\log_a ( \frac Y X) = \log_a Y - \log_a X \tag{2.4}
$$
式 \((2.4)\) で \(Y=1\) のとき、 \(log_a Y = log_a 1 = 0\) となるので
$$
\log_a ( \frac 1 X) = -\log_a X \tag{2.5}
$$
累乗の対数
$$
\log_a (X^{Y}) = Y \log_a X \tag{2.6}
$$
底の変換公式
$$
\log_a b = \frac {\log_c b} {\log_c a} \tag{2.7}
$$
\(c\) は新しい底。 \(a\) と \(b\) が以下のように移動するのが底の変換公式です。
さらっと書きましたが、このテクニックは今回に限らず色々なところで役立ちますので、↓を忘れないようにしましょう。
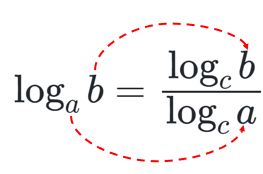
3. 対数関数の微分
さて、以下が対数関数の微分の公式です。
対数関数の微分の公式
$$
f(x) = \log_a x
$$
を \(x\) で微分した \(f'(x)\) は
$$
f'(x) = \frac{1}{x \log_e a} \tag{3.1}
$$
となります
\(e\) を底とする対数関数
$$
g(x) = \log_e x
$$
を \(x\) で微分した \(g'(x)\) は
$$
g'(x) = \frac{1}{x} \tag{3.2}
$$
となります。
なぜなら式 \((3.1)\) の \(a\) に ネイピア数 \(e\) を代入して \(g'(x) = \frac{1}{x \log_e e}\) であるが、 \(\log_e e = 1\) であるので \(g'(x) = \frac{1}{x}\) が導けるというわけす。
4. 対数関数の微分を導出する
さて、先に微分の公式を示してしまいましたが、そこまでは前菜。
ここがメインディッシュです。
前述した対数関数の微分の公式 式 \((3.1)\) を、いままで見てきた道具を使って導き出していきましょう
$$
f(x) = \log_a x
$$
を微分の公式にあてはめると
$$
\begin{aligned}
f'(x) = &\lim_{h \to 0} \frac {f(x+h)-f(x)} {h}& \
=& \lim_{h \to 0} \frac {\log_a (x+h) - \log_a x} {h} &\
\end{aligned}
$$
となるので、 \(\frac {1}{h}\) をつかった表現にすると
$$
f'(x) = \lim_{h \to 0} \frac {1} {h} (\log_a (x+h) - \log_a x) \tag{4.1}
$$
となります。
ここで、
\((x+h) = Y\)、 \(x = X\) と置くと
$$
\log_a (x+h) - \log_a x = \log_a Y - \log_a X
$$
となります。
商の対数 の公式 \((2.4)\)
$$
\log_a ( \frac Y X) = \log_a Y - \log_a X \tag{2.4}
$$
を活用すると \(\log_a Y - \log_a X\) は \(\log_a ( \frac Y X)\) となるので
ここまでの展開を列挙すると
$$
\begin{aligned}
&\log_a (x+h) - \log_a x&\
= &\log_a Y - \log_a X& \
= &\log_a ( \frac Y X)&
\end{aligned}
$$
となります。
ここで、 \(X = x\) と \(Y= (x+h)\) だったので、
$$
\begin{aligned}
\log_a ( \frac Y X)= \log_a ( \frac {x+h}{x})\
\end{aligned}
$$
となるので、ここまでの展開を再度列挙すると
$$
\begin{aligned}
&\log_a (x+h) - \log_a x&\
= &\log_a Y - \log_a X& \
= &\log_a ( \frac Y X)&\
= &\log_a ( \frac {x+h}{x})&
\end{aligned}
$$
となります。
これを式 \((4.1)\) に反映すると、
$$
f'(x) = \lim_{h \to 0} \frac {1} {h} (\log_a (x+h) - \log_a x) = \lim_{h \to 0} \frac {1} {h} (\log_a ( \frac {x+h}{x})) \tag{4.2}
$$
となります。
累乗の対数 の公式 \((2.6)\) より \(Y \log_a X = \log_a (X^{Y})\) なので、\(Y = \frac {1}{h}\) 、 \(X=\frac {x+h}{x}\) とおくと
$$
\begin{aligned}
f'(x) = &\lim_{h \to 0} \frac {1} {h} (\log_a ( \frac {x+h}{x}))
= \lim_{h \to 0} Y (\log_a X)
= \lim_{h \to 0} (\log_a(X^{Y}))&\
\
&となるので、X と Y を戻すと、&\
\
& \lim_{h \to 0} Y (\log_a X) = \lim_{h \to 0} (\log_a(\frac {x+h}{x})^\frac {1} {h}) となります。& \
\
さらに &\frac {x+h}{x} = 1 + \frac {h}{x} なので、&\
\
&\lim_{h \to 0} (\log_a(\frac {x+h}{x})^\frac {1} {h}) = \lim_{h \to 0} (\log_a(1 + \frac {h}{x})^\frac {1} {h})&\
\
&さらに、 \frac{h}{x} = t と置き換えると、&\
&\lim_{h \to 0} →\lim_{t \to 0} となり、 \frac {1} {h} → \frac {1} {tx} となるため &\
\
&\lim_{h \to 0} (\log_a(1 + \frac {h}{x})^\frac {1} {h}) = \lim_{t \to 0} (\log_a(1 + t)^{\frac {1} {tx}}) = \lim_{t \to 0} (\log_a(1 + t)^{\frac {1} {t} \cdot \frac {1} {x}})&\
\end{aligned}
$$
指数関数の公式1.4より \((a^{x})^{y} = a^{xy}\) なので、
$$
\begin{aligned}
f'(x) = &\lim_{t \to 0} (\log_a(1 + t)^{\frac {1} {t} \cdot \frac {1} {x}}) = \lim_{t \to 0} (\log_a ((1 + t)^{\frac {1} {t}})^{\frac {1} {x}})\&
\
\end{aligned}
$$
$$
\begin{aligned}
上式で & \lim_{t \to 0} (1 + t)^{\frac {1}{t}} を e とすると &\
f'(x)=&\lim_{t \to 0} (\log_a ((1 + t)^{\frac {1} {t}})^{\frac {1} {x}})=
\log_a e^{\frac {1}{x}}&
\end{aligned}
$$
さらに 累乗の対数 の公式 \((2.6)\) より
\(\log_a (X^{Y}) = Y \log_a X\) なので、 \(Y = \frac {1}{x}\) 、 \(X = e\) とおくと
$$
f'(x) = \log_a e^{\frac {1}{x}} = \frac{1}{x} \log_a {e} \tag{4.3}
$$
ここで式 \((4.3)\) にある \(\log_a {e}\) に着目する
底の変換公式 式 \((2.7)\) より \(\log_a b = \frac {\log_c b} {\log_c a}\) であるので、 \(b = e\) 、 \(c=e\) とすると
$$
\begin{aligned}
\log_a e = \frac {\log_e e}{\log_e a}
\end{aligned}
$$
となります。
$$
\begin{aligned}
\log_e e = 1 なので&\
&\frac {\log_e e}{\log_e a} = \frac {1}{log_e a}&
\end{aligned}
$$
となり、これで
$$
\log_a e = \frac {1}{log_e a}
$$
であることがわかります。式 \((4.3)\) を \(\log_a e → \frac {1}{log_e a}\) と変形すると
$$
\begin{aligned}
f'(x) = &\frac{1}{x} \log_a {e}&\
=&\frac{1}{x} \cdot \frac {1}{log_e a}&
\end{aligned}
$$
となり、式 \((3.1)\) を導くことができました。
$$
f'(x) = \frac{1}{x \log_e a} \tag{3.1、再掲}
$$
ここまでの導出過程は実際に紙に書いてやってるみるのがオススメです。
なぜなら、類似の導出が今後の LLM 系のテクニックで登場します。
論文や解説などでは、この導出の5,6ステップをしれっと飛ばしていることが多いため、そういう部分でつまづかないために、この基礎段階で1歩ずつ導出していくクセをつけておくと良いと思います。
それではまた次回お会いしましょう!
navigation




