[AI数理]徹底的に交差エントロピー(1)

おはようございます！(株) Qualiteg 研究部です。

今日からは交差エントロピーについて、徹底的に学んでいきたいとおもいます。

交差エントロピー関数の式は２つあるの？

本シリーズではは、機械学習で分類問題の損失関数としてよく使用される交差エントロピー関数をとりあげます。

実はこれまで学んできた　指数関数や対数関数の微分法は、この交差エントロピー関数を深く理解するためのものでした。

交差エントロピーがどのような性質をもっていて、どのように導かれていくのかを理解するのは今後のLLMの仕組み解明でも大いに役立つのでしっかりみていきたいとおもいます！

さて、さっそくですが、

下の \((1)\) は 交差エントロピー関数 です

$$
\ - \frac{1}{N} \sum_{i}^{N} \sum_{k}^{K} t_{ik} \log y_{ik} \tag{1}
$$

下の \((2)\) も、 交差エントロピー関数　です。

$$
\ - \frac{1}{N} \sum_{i}^{N} \lbrack t_{i} \log y_{i} + (1- t_{i}) \log (1- y_{i}) \rbrack \tag{2}
$$

「交差エントロピー関数」 で検索すると、だいたい上の2式が紹介されています。

「え？定義が2つあるの？」と素朴な疑問も浮かびますが、実はどちらも同じところから導き出すことができます。

式の単なる暗記よりもどういう素性のものなのか脳ミソに染み込ませたいので、式の導出過程を省略せずに一歩ずつ展開していって、しっかりと概念を理解したいとおもいます。

そのため同じようなことをクドクド、しつこく、繰り返し見て考えていきます！

なお、先にネタバレすると、 \((1)\) 式は 多値分類向け交差エントロピー (多値分類＝入力データを複数のクラスのどれかに分類するタスク）に使えるもので、 \((2)\) 式は 二値分類用の交差エントロピー で二値分類用（入力を２つのクラスに分類するタスク）に使えるものです。

\((2)\) 式の二値交差エントロピー関数 は、 \((1)\) 式の多クラス分類用の交差エントロピーを二値分類という特殊ケース用に式展開したもので \((1)\) 式 から簡単に導出することができます。
その展開方法も、のちほど詳しく説明します。

本シリーズで理解したいこと

• 交差エントロピー関数って２つあるみたいけど、どっちが正解なの？　という素朴な疑問が解決する

• 交差エントロピー(Cross Entropy)と 多値用交差エントロピー(Categorical Cross Entropy)と二値用交差エントロピー(Binary Cross Entropy)の違いと使いどころが理解できる

• そもそも交差エントロピーって一体何者？　どこから導き出されたものなの？が理解できる

1章 分類問題で使う交差エントロピー

ニューラルネットワークで使用する損失関数は多種多様にありますが、分類問題でのド定番は 交差エントロピー誤差関数 だとおもいます。

各種フレームワークにも必ず実装されており、「まず Deep Learning をやってみよう」というシーンでは必ずお世話になります。

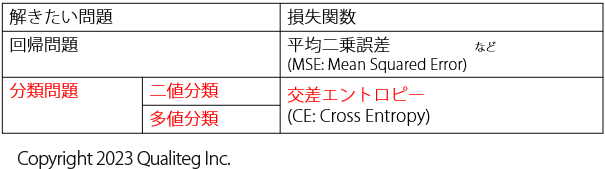
分類問題はおおきく２つに分けられます。

• 二値分類 (2クラス分類)
  • 入力データを2つのクラスのどちらに所属するのかを予測します。
    2クラス分類 ともよびます。
    二値分類は結果が「YES」なのか「No」なのかを予測することができます。
    データサイエンスのチュートリアルで有名な　「タイタニック号の乗客が生存できたか、できなかったか」 も二値分類の問題です。

【二値分類の例】

• 「このメールはスパムなのかスパムじゃないのか」
• 「このお客は買うのか買わないのか」
• 「この生徒は合格するのか、しないのか」
• 「映画レビューの感想が肯定的か否定的か」

• 多値分類 （多クラス分類)
  • 入力データが複数あるクラスのどのクラスに所属してるのかを予測します。二値分類とは違い、クラスは複数あってかまいませんが、何個のクラスに分類するかは事前に決めておきます。
    たとえば、入力した画像データが
    「イヌ」「キツネ」「オオカミ」「ネコ」「タヌキ」 の5個のクラスのうちどのクラスに所属するのかを予測する、といった具合になります。

この二値分類と多値分類の学習で使う 損失関数 が 交差エントロピー誤差関数 (cross entropy loss function) です。

多値分類（多クラス分類）と二値分類(2クラス分類)を分けていますが、論理的に考えてみれば、多値分類はその名の通り入力データが複数のクラスのうち、どのクラスに所属するかを予測するものなので、二値分類は多値分類の中に入ります。仮に分類したいクラスの数を \(k\) 個　とおけば、 \(k=2\) のときが二値分類になるということになります。 そして、 \(k>2\) がいわゆる多クラス分類になります。

このように論理的には二値分類は多値分類の特殊ケースと考えられますが、一見すると以下のように別の交差エントロピー誤差関数が使われます。

これはなぜでしょうか？・・・

ということも含めて 交差エントロピー が最終的にクリアになるように数式を丁寧にひもときつつみていきます。

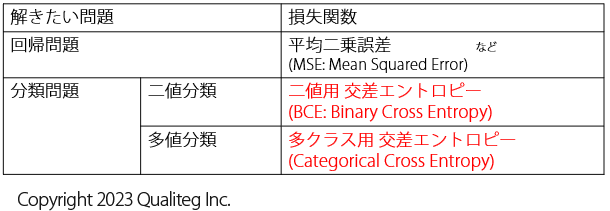
二値分類用の交差エントロピー誤差関数 は Binary Cross Entropy （バイナリクロスエントロピー）という呼称がつかわれ Deep Learning のフレームワーク等では \(BCE\) の略語で実装されています。
（binary は　バイナリ　と読み、二値とか、二成分とか、二元みたいな意味になります。入力データを「AかAじゃないか」の２通りに見分けるのでその通りな名前ですね）

$$
\ - \frac{1}{N} \sum_{i}^{N} \lbrack t_{i} \log y_{i} + (1- t_{i}) \log (1- y_{i}) \rbrack \tag{2、再掲}
$$

多値分類用の交差エントロピー誤差関数 は Categorical Cross Entropy や Multi-Class Cross Entropy という呼称がつかわれます。

$$
\ - \frac{1}{N} \sum_{i}^{N} \sum_{k}^{K} t_{ik} \log y_{ik} \tag{1、再掲}
$$

さて、今回は、交差エントロピー誤差関数がどのような問題で活躍しているか概観してまいりました。

次回は、分類問題の本質と尤度関数についてみていきたいとおもいます。

それでは、また次回お会いしましょう！

参考文献
https://blog.qualiteg.com/books/

navigation