[AI数理]徹底的に交差エントロピー(6)

おはようございます！(株) Qualiteg 研究部です。

今回は、二値分類用の交差エントロピーについてみていきましょう！

7章 二値分類用 交差エントロピー

7-1. 二値分類用 交差エントロピー (データ1件対応版)

さて、ここから、二値分類用の交差エントロピーを導きたいとおもいます。

二値分類は 入力されたデータが 2 つのうちどちらか、を予測するものです。

まず話をシンプルにするために、バッチ版ではなく、式 \((5.2)\) に示した 1件版の交差エントロピーの式を思い出します。

$$
E = - \sum_{k=1}^{K} t_{k} \log y_{k} \tag{5.2、再掲}
$$

$$
\begin{aligned}
&K:分類の数,　t_{k}:正解ラベル,　y_{k}:モデルが計算した予測値&
\end{aligned}
$$

二値分類も多値分類の一種と考えれば、式 \((5.2)\) のままで良いはずです。

つまり、多値分類の場合は \(K \ge 3 \) となりますが、これを二値分類のときは分類数は2なので \(K=2\) となります。

そこで \(K=2\) のときの交差エントロピーを \(BCE\) として、 式 \((5.2)\) 展開すると。

(BCE は Binary Cross Entropy = 二値分類用交差エントロピー　の略からとっています)

$$
\begin{aligned}
\ BCE = &- \log L&\
\ = &- \sum_{k=1}^{2} t_{k} \log y_{k}&\
\ = &- (t_{1} \log y_{1} + t_{2} \log y_{2} ) &\
\end{aligned}
$$

のようになりました。

$$
\ BCE =- (t_{1} \log y_{1} + t_{2} \log y_{2} ) \tag{7.1}
$$

ここでは2値分類用のデータとして、冒頭でも紹介した「タイタニック号の乗客が助かったか、助からなかったか」のどちらかを予測する分類問題を考えてみます。

データ参照元は以下となります

Author: Frank E. Harrell Jr., Thomas Cason
Source:?Vanderbilt Biostatistics
(http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.html)

まず「助かった」乗客のデータとモデルの予測値が以下のようだった場合、

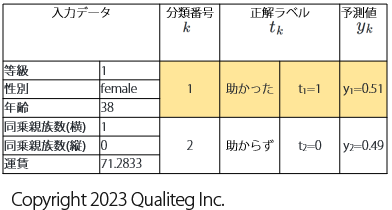
交差エントロピー \(BCE\) を計算すると

$$
\begin{aligned}
\ \ BCE =&- (t_{1} \log y_{1} + t_{2} \log y_{2} )&\
=&- (1 \cdot \log 0.51 + 0 \cdot \log 0.49 )&\
=&- \log 0.51&\
\end{aligned}
$$

同様に、今度は「助からなかった乗客」をあらわす以下のデータで交差エントロピーを計算します

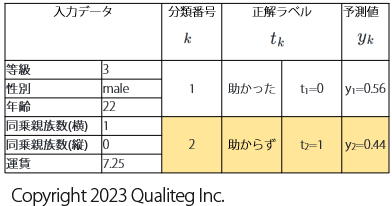
$$
\begin{aligned}
\ \ BCE =&- (t_{1} \log y_{1} + t_{2} \log y_{2} )&\
=&- (0 \cdot \log 0.56 + 1 \cdot \log 0.44 )&\
=&- \log 0.44&\
\end{aligned}
$$

このように多値分類の作法でも二値分類の交差エントロピーを計算することは当然可能です。

ところで、確率を求める分類問題の場合は予測値の合計値は 1 となります。

また、正解ラベルは正解のときに1、それ以外には0を指定していますので、その合計値も 1 となります。

つまり、二値問題の場合は

$$
y_{1} + y_{2} = 1
$$

$$
t_{1} + t_{2} = 1
$$

となるため、

$$
y_{2} = 1-y_{1}
$$

$$
t_{2} = 1-t_{1}
$$

となります。

これを式 \((7.1)\) で示した \(K=2\) のときの 交差エントロピーの式 \(BCE =- (t_{1} \log y_{1} + t_{2} \log y_{2})\) に代入すると

$$
\begin{aligned}
BCE =&- (t_{1} \log y_{1} + t_{2} \log y_{2} )&\
=&- (t_{1} \log y_{1} + (1-t_{1}) \log (1-y_{1}) )&
\end{aligned}
$$

となり、 \(t_{1}\) 、 \({y_{1}}\) だけをつかった式に変形することができます。

$$
BCE=- (t_{1} \log y_{1} + (1-t_{1}) \log (1-y_{1}) ) \tag{7.2}
$$

さて、式 \((7.2)\) からわかるように、
1件のデータに対して正解ラベルおよび予測値は　\(t_{1}\) 、 予測値 \(y_{1}\) だけとなりました。
( \(t_{2}\) や \(y_{2}\) は式変更により無くなりました)

よって正解ラベル \(t_{1}\) 、 予測値 \(y_{1}\) のように 添え字 「 \(_{1}\) 」　を付与する必要もないので、正解ラベルおよび予測値は \(t\) 、 \(y\) と添え字なしにします。

こうしてできた式 \((7.3)\) が 二値分類用の交差エントロピー関数(データ1件分)となります。

$$
BCE=- (t \log y + (1-t) \log (1-y) ) \tag{7.3}
$$

$$
t:正解ラベル y:予測値
$$

二値分類で \((7.3)\) を損失関数として使うモデルの入力データおよび正解ラベル、予測値は以下のようになります。

この入力データはタイタニックに乗船していて　「助かった」＝ \(t=1\) という正解ラベルがつきました

つまり多値分類のときは、分類数のぶんだけ正解ラベルが \(t_{1}\) 、 \(t_{2}\) 、、、のようにありましたが、二値分類の場合は　入力データを \(1\) と予測させたい場合は \(t=1\) 、入力データを \(0\) と予測させたい場合は \(t=0\) となります。

7-2. 二値分類用 交差エントロピー (データN件対応版)

さて式 \((7.3)\) はデータ1件版の交差エントロピー関数でしたが、これをN件のデータに対応した二値分類用交差エントロピー関数に拡張します。

$$
BCE=- (t \log y + (1-t) \log (1-y) ) \tag{7.3、再掲}
$$

バッチ学習で使う複数件の訓練データは以下のようになります。ここでは4件ぶん表示しました。

データ番号 \(i\) を付与しています。前述したとおし二値分類用の正解ラベル、予測値はデータ1件につき1件なので、正解ラベルと予測値はデータ番号 \(i\) を付与すれば、一意に識別できるようになります。

そこで、正解ラベル \(t\) は データ番号 \(i\) を添え字として追加して \(t_{i}\) に。予測値 \(y\) にも データ番号 \(i\) を添え字として追加して \(y_{i}\) となります。

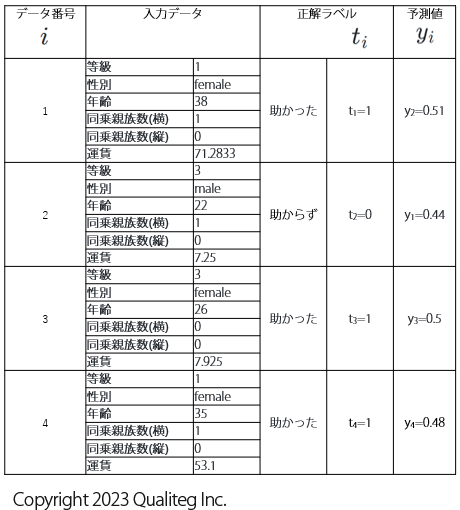
ということで、1件あたりの二値分類用交差エントロピー関数は、データ番号 \(i\) の添え字を追加して以下のようになります。

$$
BCE_{i}=- (t_{i} \log y_{i} + (1-t_{i}) \log (1-y_{i}) )
$$

あとはこれを データ数 N 件分合計したあと、データ数の影響を除くために N でわってあげれば、多値分類のときとおなじ バッチ対応版の二値分類用交差エントロピーの計算式となります。

$$
\begin{aligned}
BCE=&- \sum_{i=1}^{N} BCE_{i}&\
&- \sum_{i=1}^{N} \lbrack t_{i} \log y_{i} + (1-t_{i}) \log (1-y_{i}) \rbrack &
\end{aligned}
$$

ということで、二値分類用交差エントロピー（バッチ対応バージョン) を導くことができました。

$$
BCE=- \sum_{i=1}^{N} \lbrack t_{i} \log y_{i} + (1-t_{i}) \log (1-y_{i}) \rbrack \tag{7.4}
$$

$$
t_{i}: i番目のデータの正解ラベル　 y_{i}:i番目のデータの予測値
$$

今回はいかがでしたでしょうか

それでは、また次回お会いしましょう！

参考文献
https://blog.qualiteg.com/books/

navigation