[AI数理]徹底的に交差エントロピー(7)

おはようございます！(株) Qualiteg 研究部です。

今回は、交差エントロピーの計算をベクトルや行列で表現する方法について説明します！

8章 交差エントロピーとベクトル演算

そもそも、なぜ、交差エントロピーをベクトルや行列で表現したいのでしょうか？

それは、実際にニューラルネットワークをコンピュータープログラムとして実装するときに、訓練データや予測値はベクトル(1次元配列)や行列(2次元配列)といったN階テンソル(N次元配列)の形式で取り扱われるからです。

なぜベクトルや行列かといえば、ニューラルネットワークの実用的な計算をするときにはデータを1件とりだしては、1件計算する　のではなく、多くのデータをベクトル（1次元配列）や行列（2次元配列）やそれ以上の多次元配列に詰めたのちに、まとめてドカっと計算するからです。

（まとめてドカっと計算するのが得意な GPU があるからこそ、これだけ Deep Learning が進展した、ともいえます）

そこで、今までで導出してきた交差エントロピーの計算をコンピュータで実装するときに備えて、 1次元配列 にしてみます。

プログラムコード上は単なる1次元配列ですが、これを配列の各値を成分にもつ ベクトル と見立てることにします。

正解ラベル \(t_{k}\) を要素に含む ベクトルを \(\boldsymbol{t}\) とすると、以下のような成分を含むベクトルになります。

$$
\boldsymbol{t} =
\begin{pmatrix}
t_{1} & t_{2} & t_{3}
\end{pmatrix}
$$

この場合、横に成分（＝数字）をならべているので、 行ベクトル(または 横ベクトル) と呼びます。

予測値 \(y_{k}\) も同様に \(\boldsymbol{y}\) として 行ベクトル にあらわすと

$$
\boldsymbol{y} =
\begin{pmatrix}
y_{1} & y_{2} & y_{3}
\end{pmatrix}
$$

となります。

さらに、交差エントロピーの計算の際、 \(\boldsymbol{y}\) の成分は 対数 \(\log\) をとることになるので、 \(\boldsymbol{y}\) の成分に \(\log\) をとったものを \(\boldsymbol{y_{l}}\) と定義すると、以下のようになります。

$$
\boldsymbol{y_{l}} =
\begin{pmatrix}
\log y_{1} & \log y_{2} & \log y_{3}
\end{pmatrix}
$$

ここで 交差エントロピー \(E\) を思い出してみます。

$$
\begin{aligned}
\ E = &- \sum_{k=1}^{K} t_{k} \log y_{k} &\
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
\end{aligned}
$$

この式にあらわれる \(( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3})\) をよく見てみましょう。これは、ベクトル \(\boldsymbol{t}\) と ベクトル \(\boldsymbol{y_{l}}\) のドット積（内積）となっているのがわかります。

ドット積（内積）は同じ添え字の成分どうしの積の足し算です。

$$
\begin{aligned}
\ E =　&- \boldsymbol{t} \cdot \boldsymbol{y_{l}}& \
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
\end{aligned}
$$

１つ注意したい点は、ベクトルの場合は　成分どうしの積の足し算と定義すればよいですが、ベクトルではなく、行列（２次元配列)どうしのドット積を計算するときには、行列の形状を意識しなければいけません。

たとえば、縦横 \(2 \times 3\) の形状をもつ行列 $\begin{pmatrix}
1 & 2 & 3 \
4 & 5 & 6 \
\end{pmatrix}\( と 縦横 \)3 \times 2\( の形状をもつ行列 \)\begin{pmatrix}
7 & 8 \
9 & 10 \
11 & 12 \
\end{pmatrix}$ のドット積

$$
\begin{pmatrix}
1 & 2 & 3 \
4 & 5 & 6 \
\end{pmatrix}
\cdot
\begin{pmatrix}
7 & 8 \
9 & 10 \
11 & 12 \
\end{pmatrix}
$$

は、以下のように計算します。

左側の行列の1行目の横一列と、右側の行列の1列目の縦一列の成分どうしの積を足していきます。

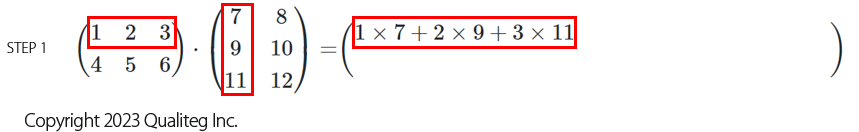
次は左側の行列の2行目と、右側の行列の1列目の成分どうしの積を足す、、、以降同様に計算していきます。

このように順に計算していくと結果は以下のようになります。

$$
\begin{aligned}
\begin{pmatrix}
1 & 2 & 3 \
4 & 5 & 6 \
\end{pmatrix}
\cdot
\begin{pmatrix}
7 & 8 \
9 & 10 \
11 & 12 \
\end{pmatrix}=&
\begin{pmatrix}
1 \times 7 + 2 \times 9 + 3 \times 11 & 1 \times 8 + 2 \times 10 + 3 \times 12 \
4 \times 7 + 5 \times 9 + 6 \times 11 & 4 \times 8 + 5 \times 10 + 6 \times 12
\end{pmatrix}&\
=&
\begin{pmatrix}
58 & 64 \
139 & 154 \
\end{pmatrix}&
\end{aligned}
$$

この例からわかる通り縦横 \(2 \times 3\) の形状をもつ行列と 縦横 \(3 \times 2\) の形状をもつ の行列のドット積の結果は \(2 \times 2\) の行列となります。

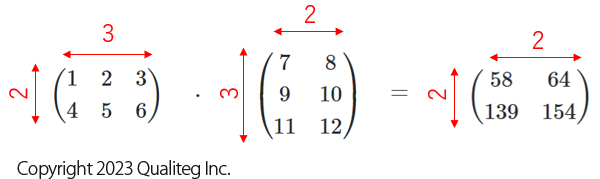
つまり \(m \times n\) と \(n \times l\) のドット積の形状は \(m \times l\) となります。
またドット積を計算するには、左側の行列の行数と、右側の行列の列数が一致している必要があります。

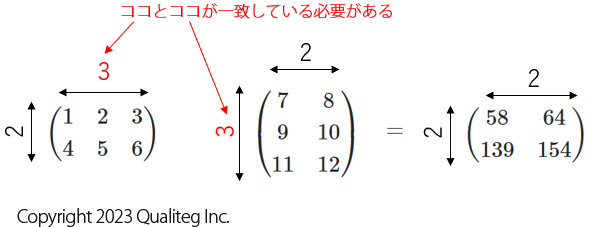
さて、行列のドット積の計算の仕方を見たところで、さきほどのベクトル同士のドット積を再確認しましょう。

正解ラベルを示す行ベクトルを \(\boldsymbol{t}\) と、予測値に \(\log\) をとった行ベクトル \(\boldsymbol{y_{l}}\) はそれぞれ以下のとおりでしたが、

$$
\boldsymbol{t} =
\begin{pmatrix}
t_{1} & t_{2} & t_{3}
\end{pmatrix}
$$

$$
\boldsymbol{y_{l}} =
\begin{pmatrix}
\log y_{1} & \log y_{2} & \log y_{3}
\end{pmatrix}
$$

さきほどの行列のドット積ルールにしたがって計算しようとすると、横一列並んでいる形状をしている行ベクトル同士の計算はできないことがわかります。

つまり、

$$
\begin{pmatrix}
t_{1} & t_{2} & t_{3}
\end{pmatrix}
\cdot
\begin{pmatrix}
\log y_{1} & \log y_{2} & \log y_{3}
\end{pmatrix}
$$

はこのままでは計算できないということになります。
つまり、この2つの行ベクトルを行列とみなすと、どちらも形状が \(1 \times 3\) となっています。

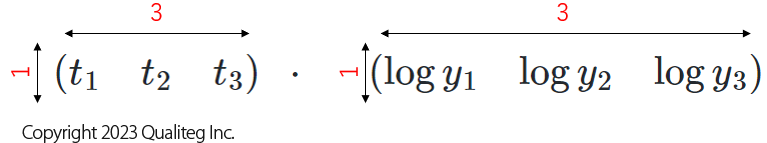
ですので、ドット積ができる行列形状である \(m \times n\) と \(n \times l\) のカタチにするには、ベクトル \(\boldsymbol{y_{l}}\) を行ベクトル（横ベクトル）から列ベクトル（縦ベクトル）にすればよさそうです。

\(\boldsymbol{y_{l}}\) の成分の行と列を入れ替えた列ベクトル　\(\boldsymbol{y_{l}^\mathsf{T} }\) は以下のようになります。

(\({\mathsf{T} }\) は転置を意味します。転置とはある行列の成分の列と縦を入れ)替えた行列です。

$$
\boldsymbol{y_{l}^\mathsf{T} } =
\begin{pmatrix}
\log y_{1} \ \log y_{2} \ \log y_{3}
\end{pmatrix}
$$

これで、ドット積の作法で計算することができるようになりました。

さきほどの、ドット積を使った交差エントロピーの計算式でみてみると、

$$
\begin{aligned}
\ E =　&- \boldsymbol{t} \cdot \boldsymbol{y_{l}^\mathsf{T} }& \
&=-\begin{pmatrix}
t_{1} & t_{2} & t_{3}
\end{pmatrix}
\cdot
\begin{pmatrix}
\log y_{1} \ \log y_{2} \ \log y_{3}
\end{pmatrix}& \
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
\end{aligned}
$$

これで、交差エントロピーを行列の計算として求めることができました。

(ちなみに、ベクトル同士のドット積は内積と同じなので計算結果はスカラー（数値）になります。)

今回はいかがでしたでしょうか

冒頭でもふれたとおり、データをベクトルや行列に見立ててドット積を計算したのは、1件ずつ計算をしてループさせるような方式よりも、ベクトルや行列にデータをまとめてイッキに計算したほうが GPU など並列計算が得意な環境では圧倒的に効率が良いためです。

ベクトルや行列にするとコンピューター(とりわけ GPU)との相性がよく計算効率・スピードを高める効果が期待できるからこそこのようなテクニックを用いていますますので、それこそが重要であり、それ以上の数学的な意味・意義はそんなに考えなくてよいのかなというところでしょうか。

それでは、また次回お会いしましょう！

参考文献
https://blog.qualiteg.com/books/