発話音声からリアルなリップシンクを生成する技術 第2回:AIを使ったドリフト補正

こんにちは!
前回の記事では、当社のMotionVoxで使用している「リップシンク」技術について、wav2vecを用いた音声特徴量抽出の仕組みを解説しました。音声から正確な口の動きを予測するための基礎技術について理解いただけたかと思います。
今回は、その続編として、リップシンク制作における重要な技術的課題である「累積ドリフト」に焦点を当てます。wav2vecで高精度な音素認識ができても、実際の動画制作では複数の音声セグメントを時系列に配置する際、わずかなタイミング誤差が蓄積して最終的に大きなずれとなる現象が発生します。
本記事では、この累積ドリフトのメカニズムと、機械学習を活用した最新の補正技術について、実際の測定データを交えながら詳しく解説していきます。前回のwav2vecによる特徴抽出と今回のドリフト補正技術を組み合わせることで、MotionVoxがどのように高品質なリップシンクを実現しているのか、その全体像が見えてくるはずです。
累積ドリフトとは何か
基本概念
累積ドリフトとは、個々の音声セグメントが持つ微小なタイミング誤差が、時間の経過とともに蓄積していく現象です。
セグメント1: +0.5ms の誤差
セグメント2: -0.3ms の誤差
セグメント3: +0.8ms の誤差
...
100セグメント後: 合計 42ms のずれ
実際の測定例
以下は、約7分間の音声コンテンツにおける累積ドリフトの実測データです
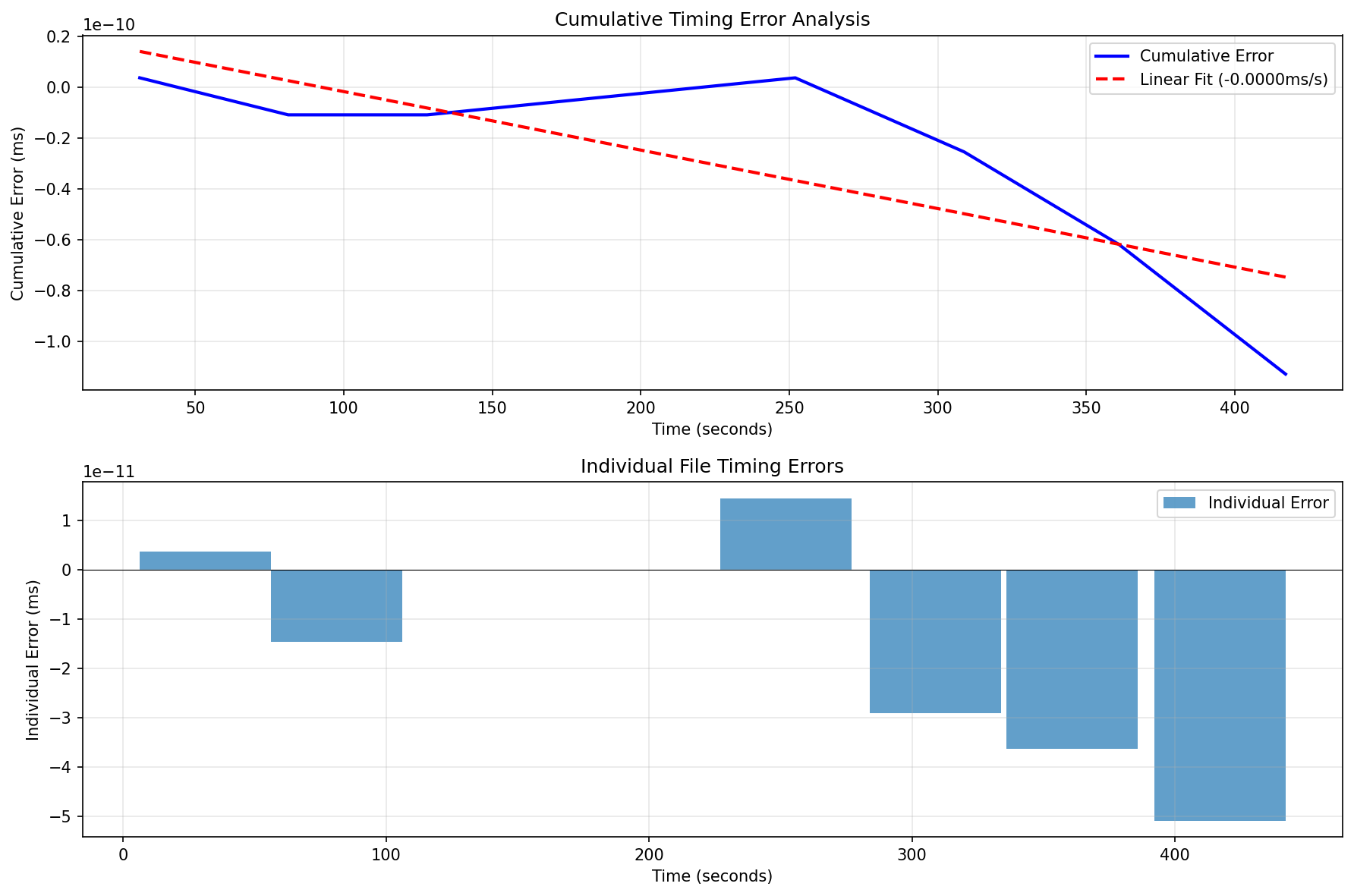
上段のグラフ:累積タイミング誤差
- 青い実線:実際の累積誤差の推移
- 赤い破線:線形近似(-0.0000ms/s)
- 縦軸のスケールは10^-10と極めて小さく、技術的にはほぼ完璧な精度
下段のグラフ:個別ファイルのタイミング誤差
- 各音声ファイルの誤差は10^-11ミリ秒オーダー
- プラスとマイナスの誤差が混在し、相殺効果が働いている
この測定結果は興味深い事実を示しています:技術的には測定限界に近い精度で同期が取れているにも関わらず、視聴時には微妙なずれを感じることがあるという現象です。
リップシンクのズレはなぜ発生するのか
1. デジタル音声の離散性
デジタル音声はサンプリング周波数によって時間分解能が決まります
# 48kHzサンプリングの場合
time_resolution = 1 / 48000 # 約0.021ms
# 1.5秒を表現しようとすると
ideal_samples = 1.5 * 48000 # 72000サンプル
actual_duration = 72000 / 48000 # 正確に1.5秒
2. ファイルフォーマットの制約
音声ファイルのヘッダー情報と実際のサンプル数の不一致
- メタデータの丸め誤差
- エンコーダーの実装差異
- フォーマット変換時の誤差
3. 処理ツールの精度
音声編集ソフトウェアやライブラリによる処理精度の違い
- フレーム境界での切り捨て/切り上げ
- 浮動小数点演算の累積誤差
- リサンプリング時の補間誤差
人間の知覚と技術的精度のギャップ
知覚閾値
人間の聴覚・視覚システムには以下の特性があります:
| 遅延時間 | 知覚への影響 |
|---|---|
| 0-20ms | ほぼ認識不可能 |
| 20-40ms | 敏感な人は違和感を感じる |
| 40-80ms | 多くの人が違和感を感じる |
| 80ms以上 | 明確にずれを認識 |
上記の測定データが示すように、技術的な誤差がほぼゼロでも知覚的な違和感が生じる理由として
- 映像処理のレイテンシ
- 再生デバイスの遅延
- 心理音響学的な要因
などが考えられます。
ドリフト分析の手法
それでは、実際のドリフト分析の手法をみていきましょう
1. 誤差の測定
まず、各音声セグメントの期待値と実測値の差を計測します
def measure_segment_error(expected_duration, actual_duration):
"""セグメントごとの誤差を測定"""
error_ms = (actual_duration - expected_duration) * 1000
return {
'absolute_error': abs(error_ms),
'signed_error': error_ms,
'relative_error': error_ms / (expected_duration * 1000)
}
2. 累積パターンの分析
次に誤差がどのように蓄積するかをモデル化します
def analyze_accumulation_pattern(errors, timestamps):
"""累積パターンを分析"""
cumulative = np.cumsum(errors)
# 線形モデル: drift = a * time + b
linear_fit = np.polyfit(timestamps, cumulative, 1)
# 二次モデル: drift = a * time² + b * time + c
quadratic_fit = np.polyfit(timestamps, cumulative, 2)
# モデルの適合度を評価
linear_r2 = calculate_r_squared(cumulative, linear_fit)
quadratic_r2 = calculate_r_squared(cumulative, quadratic_fit)
return {
'pattern': 'linear' if linear_r2 > 0.9 else 'nonlinear',
'drift_rate': linear_fit[0], # ms/秒
'acceleration': quadratic_fit[0] if quadratic_r2 > linear_r2 else 0
}
3. 統計的特性の把握
最後に統計的な特性を把握します
def statistical_analysis(errors):
"""誤差の統計的特性を分析"""
return {
'mean': np.mean(errors),
'std': np.std(errors),
'skewness': scipy.stats.skew(errors),
'is_systematic': abs(np.mean(errors)) > np.std(errors) / 2
}
さて、ここまででズレを分析する手法をみてきました。
では、そのズレを補正する手法を簡単にみていきましょう。まずはクラシックな手法からみていきます
従来の補正手法
ドリフト分析によって累積誤差のパターンが明らかになったら、次はその補正です。機械学習を導入する前に、まず従来から使われている基本的な補正手法について理解しておきましょう。これらの手法は計算が軽量で実装もシンプルなため、多くの場面で今でも有効に機能します。
1. 静的オフセット補正
全体に一定の補正を適用
def static_offset_correction(position, offset_ms, sample_rate):
"""固定オフセットによる補正"""
offset_samples = int(offset_ms * sample_rate / 1000)
return position + offset_samples
適用場面
- 系統的な遅延/進みがある場合
- ドリフト率が非常に小さい場合
2. 線形補正
時間に比例した補正を適用
def linear_correction(position, time, drift_rate, sample_rate):
"""線形ドリフト補正"""
# drift_rate: ms/秒
correction_ms = -drift_rate * time
correction_samples = int(correction_ms * sample_rate / 1000)
return position + correction_samples
適用場面
- 一定速度でドリフトが進行する場合
- 長時間コンテンツでの累積誤差
3. 適応的補正
セグメントごとに最適な補正を計算
def adaptive_correction(segments, measured_errors):
"""適応的補正アルゴリズム"""
corrections = []
accumulated_error = 0
for i, segment in enumerate(segments):
# 現在までの累積誤差
accumulated_error += measured_errors[i]
# 将来の誤差を予測
future_segments = len(segments) - i - 1
predicted_future_error = np.mean(measured_errors) * future_segments
# 最適な補正量を計算
optimal_correction = -(accumulated_error + predicted_future_error * 0.5)
corrections.append(optimal_correction)
return corrections
4. スプライン補間による滑らかな補正
from scipy.interpolate import UnivariateSpline
def spline_correction(timestamps, cumulative_errors, smoothing_factor=0.1):
"""スプライン補間による滑らかな補正"""
# 補正曲線を生成
spline = UnivariateSpline(timestamps, -cumulative_errors,
s=smoothing_factor)
# 各時点での補正値を計算
corrections = spline(timestamps)
return corrections
従来手法の限界と機械学習への期待
ここまで見てきた従来の補正手法は、多くの場合において十分な効果を発揮します。特に、ドリフトパターンが単純で予測可能な場合は、これらの手法だけで高品質なリップシンクを実現できます。
しかし、実際の制作現場では以下のような複雑な状況に直面することがあります
- 非線形で複雑なドリフトパターン➡単純な数式では表現できない複雑な誤差の蓄積
- コンテンツ依存の変動➡ 話者の特性、発話速度、感情表現などによって変化するドリフト
- 予測困難な外乱➡ エンコーディング、編集処理、再生環境による予期せぬ遅延
これらの課題に対して、従来手法では限界があります。そこで注目されているのが、機械学習を活用した次世代のドリフト補正技術です。大量のデータから複雑なパターンを学習し、未知の状況にも適応できる柔軟性を持つ機械学習は、リップシンク品質のさらなる向上を約束してくれます。
機械学習を用いた高度な補正
従来の補正手法では対応が困難な複雑なドリフトパターンに対して、機械学習は革新的なアプローチを提供します。
ここからは、AIの力を借りることで、どのように高度なドリフト補正が可能になるのかを見ていきましょう。
機械学習の最大の強みは、明示的にプログラミングすることなく、データから複雑なパターンを自動的に学習できる点です。リップシンクのドリフト補正においては、過去の大量のプロジェクトデータから「どのような状況でどのようなドリフトが発生するか」を学習し、新しいコンテンツに対しても適切な補正を予測できるようになります。
1. LSTM による時系列予測
累積ドリフトのパターンを学習し、将来の誤差を予測
import tensorflow as tf
class DriftPredictionLSTM:
def __init__(self, sequence_length=10):
self.model = tf.keras.Sequential([
tf.keras.layers.LSTM(64, return_sequences=True),
tf.keras.layers.LSTM(32),
tf.keras.layers.Dense(16, activation='relu'),
tf.keras.layers.Dense(1)
])
def train(self, historical_errors, timestamps):
"""過去のプロジェクトのドリフトパターンを学習"""
X, y = self.create_sequences(historical_errors)
self.model.compile(optimizer='adam', loss='mse')
self.model.fit(X, y, epochs=100, validation_split=0.2)
def predict_drift(self, recent_errors):
"""次のセグメントのドリフトを予測"""
return self.model.predict(recent_errors.reshape(1, -1, 1))
2. 強化学習による適応的補正
環境からのフィードバックを基に補正戦略を最適化
class AdaptiveCorrectionRL:
def __init__(self, state_dim=5, action_dim=11):
# 状態: [累積誤差, 現在位置, 誤差の分散, 残りセグメント数, 前回の補正量]
# 行動: -5ms から +5ms の補正(1ms刻み)
self.q_network = self.build_q_network(state_dim, action_dim)
self.memory = []
def build_q_network(self, state_dim, action_dim):
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation='relu', input_shape=(state_dim,)),
tf.keras.layers.Dense(32, activation='relu'),
tf.keras.layers.Dense(action_dim)
])
return model
def choose_action(self, state, epsilon=0.1):
"""ε-greedy方策で補正量を決定"""
if np.random.random() < epsilon:
return np.random.randint(-5, 6) # 探索
else:
q_values = self.q_network.predict(state.reshape(1, -1))
return np.argmax(q_values) - 5 # 活用
def update(self, state, action, reward, next_state):
"""Q値を更新"""
# Deep Q-Learning のアップデート処理
pass
3. 畳み込みニューラルネットワークによるパターン認識
音声波形から直接ドリフトパターンを検出
class WaveformDriftDetector:
def __init__(self):
self.model = tf.keras.Sequential([
# 1D畳み込みで波形の特徴を抽出
tf.keras.layers.Conv1D(32, 128, activation='relu'),
tf.keras.layers.MaxPooling1D(4),
tf.keras.layers.Conv1D(64, 64, activation='relu'),
tf.keras.layers.GlobalMaxPooling1D(),
# 全結合層で誤差を予測
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dropout(0.5),
tf.keras.layers.Dense(1) # 予測誤差(ms)
])
def detect_inherent_delay(self, waveform):
"""波形から固有の遅延を検出"""
# 音声の立ち上がり特性などから
# エンコーディングに起因する遅延を推定
features = self.extract_features(waveform)
return self.model.predict(features)
4. アンサンブル学習による堅牢な補正
複数の手法を組み合わせて信頼性を向上
class EnsembleDriftCorrector:
def __init__(self):
self.correctors = [
LinearCorrector(),
SplineCorrector(),
LSTMPredictor(),
RLCorrector()
]
self.weights = [0.25, 0.25, 0.25, 0.25]
def correct(self, segment_info):
"""複数の補正手法の重み付き平均"""
corrections = []
for corrector, weight in zip(self.correctors, self.weights):
correction = corrector.predict(segment_info)
corrections.append(correction * weight)
# 外れ値を除外した平均
final_correction = np.median(corrections)
return final_correction
def adapt_weights(self, performance_metrics):
"""各手法の性能に基づいて重みを調整"""
# メタ学習により最適な重みを学習
pass
機械学習手法の実践的価値
このように機械学習ベースの補正手法は、従来手法では不可能だった以下の価値を提供します
1. 複雑性への対応力
- 非線形で予測困難なドリフトパターンも学習可能
- 複数の要因が絡み合った複合的な誤差にも対応
2. 適応性と汎化性能
- 新しいタイプのコンテンツや話者にも柔軟に適応
- 学習データが増えるほど精度が向上する成長型システム
3. 自動化と効率化
- 手動でのパラメータ調整が不要
- リアルタイムでの高速処理も実現可能
4. 継続的な改善
- フィードバックループによる自己改善
- 最新のデータトレンドを常に反映
これらの機械学習手法は、単独でも強力ですが、従来手法と組み合わせることで、さらに堅牢で実用的なシステムを構築できます。例えば、基本的な線形補正で大まかな調整を行い、残った複雑な誤差パターンを機械学習で補正するハイブリッドアプローチも有効です。
次のセクションでは、これらの技術を実際のワークフローに組み込む際の実装上の考慮事項について詳しく見ていきます。
実践的なワークフロー
ここまで従来手法と機械学習による補正技術について解説してきましたが、実際の制作現場では、これらの技術をどのように組み合わせて活用するのでしょうか。ここでは、理論を実践に落とし込むためのワークフローについて説明します。
効果的なドリフト補正は、単一の技術に頼るのではなく、状況に応じて適切な手法を選択し、組み合わせることが重要です。以下にMotionVoxでの実践経験に基づいた、段階的アプローチをご紹介します。
- 初期分析
- 全セグメントの誤差測定
- 累積パターンの特定
- 機械学習モデルの訓練データ準備
- 補正戦略の選択
- 線形ドリフト → 線形補正 + LSTM予測
- ランダム誤差 → 適応的補正 + 強化学習
- 複雑なパターン → アンサンブル手法
- パラメータ調整
- 機械学習モデルのハイパーパラメータ
- 補正の強度と平滑化
- 検証とフィードバック
- A/Bテストによる知覚評価
- モデルの継続的な改善
さらなる改善に向けて
現在のワークフローは十分実用的ですが、将来的にはさらなる進化が期待されます。問題の種類を瞬時に判定して最適な補正手法を自動選択するリアルタイム診断システムや、人間の視聴覚認知モデルを組み込むことで技術的精度と体感品質のギャップを解消する仕組みの実装が考えられます。また、軽量化したモデルによるエッジデバイスでのリアルタイム処理の実現や、AIがなぜその補正を選択したのかを説明できる機能により、クリエイターとAIのより良い協働が可能になるでしょう。これらの改善により、より直感的で高速、かつ信頼性の高いリップシンクシステムの実現を目指していきます。
まとめ
リップシンクの品質は、視聴者の没入感を大きく左右する重要な要素です。本記事で見てきたように、技術的には極めて高い精度で音声同期が可能になっている一方で、人間の知覚を完全に満足させるにはさらなる工夫が必要です。
機械学習の導入により、従来の決定論的なアプローチでは対応困難だった以下の課題に対処できるようになりました
- 非線形なドリフトパターンの予測と補正
- コンテンツ特性に応じた適応的な調整
- 過去のプロジェクトからの学習による精度向上
- リアルタイム処理における高速な意思決定
今後は事前生成したフォトリアルアバターだけでなくメタバース空間でのリアルタイムアバター制御など、より高度なリップシンクが求められる場面が増えていくでしょう。機械学習モデルの進化と、人間の知覚モデルのより深い理解とリアリティへの執念wにより、完全に自然なリップシンクの実現を目指していきたいとおもいます!
それでは、次回またお会いしましょう!




