[AI数理]徹底的に交差エントロピー(4)

おはようございます！(株) Qualiteg 研究部です。

今回は、多値分類用の交差エントロピーを計算していきたいと思います！

5章 多値分類用 交差エントロピーの計算 (データ1件対応版)

まず 交差エントロピー関数（標本データ１件ぶんバージョン)　を再掲します。

$$
\ - \log L=\sum_{k=1}^{K} t_{k} \log y_{k} \tag{4.3、再掲}
$$

$$
t_{k} :頻度, y_{k}:確率
$$

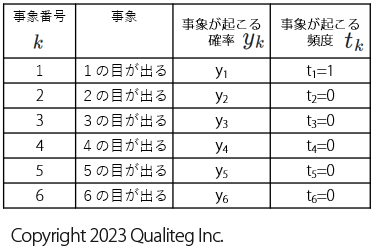
式 \((4.3)\) の 交差エントロピー は 1件の標本データ に \(K\) 個の事象（が起こったか、起こらなかったか）が含まれていました。

サイコロでいえば、1回試行したときに \(K=6\) 通りの目の出方があるということです。それぞれの変数は \(y_{k} :\) 確率、 \(t_{k} :\) 頻度, となりました。

さて、これまでの過程をふまえて、
ここからは、確率 の頭から 分類問題 の頭に切り替えていきたいと思います。

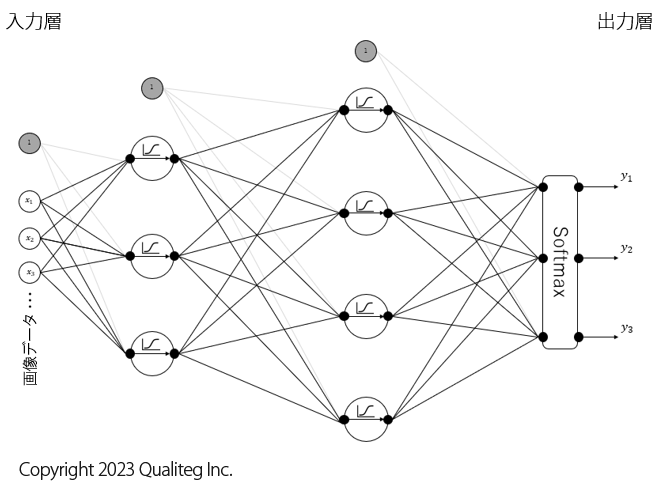
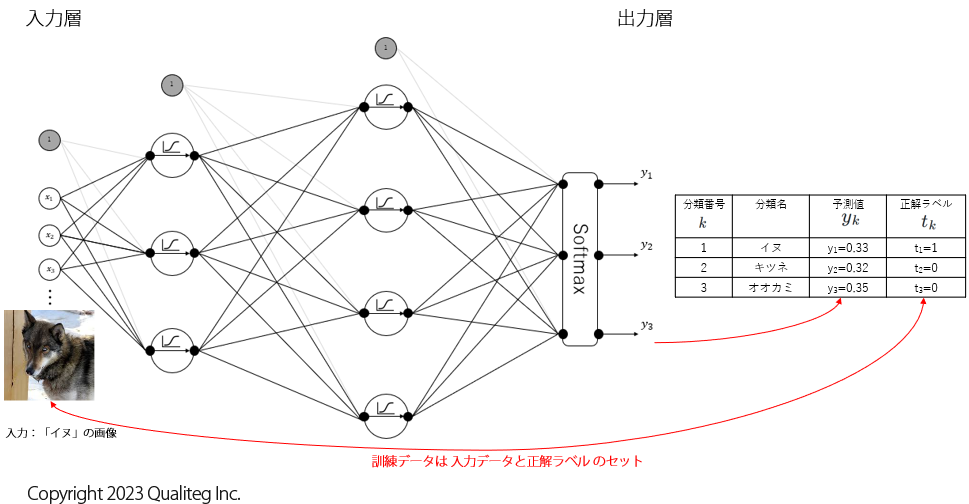
さて、ここで以下のようなニューラルネットワークのモデルを考えます。（モデルの詳細は重要ではないです）

このモデルは画像データを入力すると、その画像が「イヌ」である確率、「キツネ」である確率、「オオカミ」である確率をそれぞれ予測します。

そして、このモデルはまだ何も学習していない状態だとします。

この状態で、とりあえず「イヌ」の画像を入れてみたら、以下のようになりました。

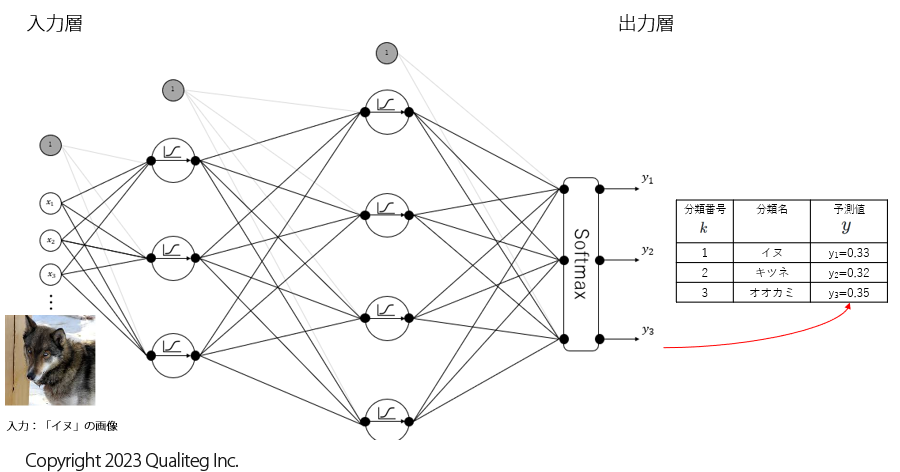
何も学習していない状態なので、このモデルが計算した予測値も正解には遠いですが、「イヌ」に相当する予測値 \(y_{1}\) は \(0.33\)、「キツネ」に相当する予測値 \(y_{2}\) は \(0.32\)、「オオカミ」に相当する予測値 \(y_{3}\) は \(0.35\) となりました。

さて、ここから、このモデルが計算した予測値が正解である確率 \(L\) を考えてみると、この例では、「イヌ」が正解で「キツネ」と「オオカミ」は不正解であることがあらかじめわかっているので、

$$
\begin{aligned}
L = &y_{1}^{1} \cdot y_{2}^{0} \cdot y_{3}^{0}&
\
=&0.33^{1} \times 0.32^{0} \times 0.35^{0}&\
=&0.33&
\end{aligned}
$$

と計算することができます。
(\(0.33\) なので、まだダメなモデルですが、計算上はこうなります。)

このように「イヌ」は正解なので \(1\)　、「キツネ」と「オオカミ」は不正解なので \(0\) とすると、正解、不正解は 正解ラベル \(t_{k}\) 列として以下のように整理できます。

そこで、確率 \(L\) を \(y_{k}\) と \(t_{k}\) であらわすと、

$$
\begin{aligned}
L = &y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}}&
\
=&\prod_{k=1}^3 y_{k}^{t_{k}} &\
\end{aligned}
$$

となります。これはサイコロの例でいう 1回の試行あたりの尤度 と同じ式になりますので、ここでもこの計算で導かれた確率を 尤度 と考えましょう。

さらにサイコロの例と同様に、さらに確率 \(L\) に対数をとって 対数尤度 の式を整理すると

$$
\begin{aligned}
\log L =&\log (y_{1}^{t_{1}} \cdot y_{2}^{t_{2}} \cdot y_{3}^{t_{3}}) & \
\
&対数の公式① 「\log ab = \log a + \log b」 より&\\
=&\log y_{1}^{t_{1}} + \log y_{2}^{t_{2}} + \log y_{3}^{t_{3}}&\
\\
&対数の公式② 「\log a^{b} = b \log a」 より&\\
=&t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}&\
\
=&\sum_{k=1}^{3} t_{k} \log y_{k}&\
\
&t_{k}:正解ラベル、y_{k}:予測値&
\end{aligned}
$$

となります。

今回は 「イヌ」「キツネ」「オオカミ」の3つの分類でしたが、添え字 \(1\) ～ \(3\) を \(K\) に置き換えて \(\sum\) であらわすと、以下のようになります。

$$
\log L = \sum_{k=1}^{K} t_{k} \log y_{k} \tag{5.1} \
$$

$$
\begin{aligned}
&K:分類の数,　t_{k}:正解ラベル,　y_{k}:予測値&
\end{aligned}
$$

これが　対数尤度関数　となります。

サイコロの例でも確認済ですが、交差エントロピー \(E\) は対数尤度関数にマイナスをつけたものなので、

$$
E = - \log L
$$

$$
E = - \sum_{k=1}^{K} t_{k} \log y_{k} \tag{5.2}
$$

$$
\begin{aligned}
&K:分類の数,　t_{k}:正解ラベル,　y_{k}:モデルが計算した予測値&
\end{aligned}
$$

これで、学習時につかう 訓練データ 1件 あたりの交差エントロピー関数 \(E\) を定義することができました。

さっそく、 式 \((5.2)\) の交差エントロピー関数 \(E\) に以下のデータを再度つかって訓練データ1件ぶんの交差エントロピー誤差 を計算してみましょう。

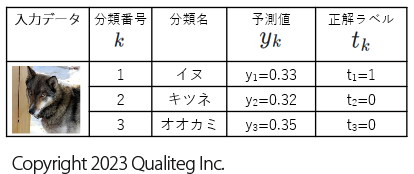
$$
\begin{aligned}
\ E = &- \sum_{k=1}^{K} t_{k} \log y_{k} &\
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
&= - ( 1 \cdot \log 0.33 + 0 \cdot \log 0.32 + 0 \cdot \log 0.35) \
&= -0.481486 \
\
&K:分類の数,　t_{k}:正解ラベル,　y_{k}:モデルが計算した予測値&
\end{aligned}
$$

この交差エントロピー誤差を損失関数として、損失関数が小さくなるようにモデルの重みパラメータを更新していくのが、基本的なニューラルネットワークの学習となります。

ちなみに、いまは以下のように訓練データ1件ぶんの学習で使う損失関数です。1件の入力データをニューラルネットワークに入力して得られた結果 \(y_{k}\) と正解ラベル \(t_{k}\) から誤差関数として交差エントロピー誤差を計算しました。

今回は、多値分類用交差エントロピーをデータ１件の場合で計算してみました。

次回は、これを N 件に拡張していきたいとおもいます。

それでは、また次回お会いしましょう！

参考文献
https://blog.qualiteg.com/books/

navigation