AI数理

[AI数理]徹底的に交差エントロピー(5)

Qualiteg 研究部

2024年4月17日 — 5 min read

おはようございます！(株) Qualiteg 研究部です。

今回は、前回から拡張してデータN件対応版の多値分類用交差エントロピーを実際のデータをみながら導いていきたいとおもいます！

6章多値分類用交差エントロピー (データN件対応版)

実際の学習では、いちどに複数件の訓練データを入力して得られた複数の結果をまとめて評価するバッチ学習を行うため、複数の訓練データから得られた結果を同時に計算できるバージョンの交差エントロピーも考えておきます。

以下のような複数の訓練データの場合を考えます。

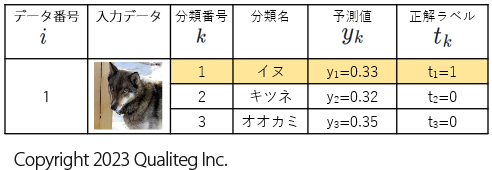
複数の訓練データなので、1件ずつの訓練データを見分けられるように番号をふった データ番号 列を導入しました。みやすくするため正解のデータに背景色をつけています。

この4件のデータを順番にモデルに入れたときの出力を計算すると以下のようになりました。予測値 列を右に追加しています。

さて、この4件の交差エントロピーを求めてみます。

これらのデータから1つずつ交差エントロピーを計算して、その値を合計すれば、4件ぶんの交差エントロピーの合計値を求めることができるので、特に難しいことはなく、1件ずつの交差エントロピーを計算して合計したいとおもいます。

まずは愚直に計算してみます。

1件目のデータの交差エントロピーを計算

1件目のデータの交差エントロピーは以下のようになります。ここでデータ番号がわかるように、交差エントロピー $E$ は $E_{1}$ としました。

$$
\begin{aligned}
\ E_{1} = &- \sum_{k=1}^{K} t_{k} \log y_{k} &\
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
&= - ( 1 \cdot \log 0.33 + 0 \cdot \log 0.32 + 0 \cdot \log 0.35) \
&= \log 0.33 = -0.481486 \
\
&K:分類の数,　t_{k}:正解ラベル,　y_{k}:モデルが計算した予測値&
\end{aligned}
$$

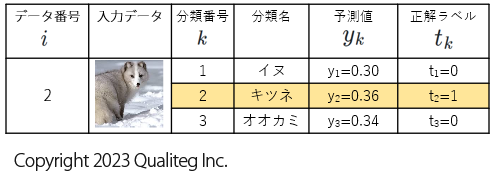
2件目のデータの交差エントロピーを計算

同様に、 $E_{2}$ を計算すると、

$$
\begin{aligned}
\ E_{2} = &- \sum_{k=1}^{K} t_{k} \log y_{k} &\
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
&= - ( 0 \cdot \log 0.30 + 1 \cdot \log 0.36 + 0 \cdot \log 0.34) \
&= \log 0.36 = -0.443697 \
\end{aligned}
$$

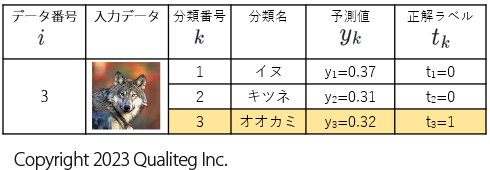
3件目のデータの交差エントロピーを計算

同様に、 $E_{3}$ を計算すると、

$$
\begin{aligned}
\ E_{3} = &- \sum_{k=1}^{K} t_{k} \log y_{k} &\
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
&= - ( 0 \cdot \log 0.37 + 0 \cdot \log 0.31 + 1 \cdot \log 0.32) \
&= \log 0.32 = -0.494850 \
\end{aligned}
$$

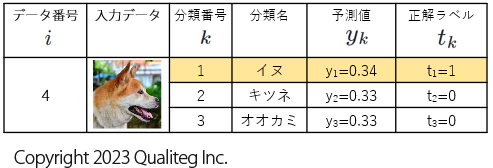
4件目のデータの交差エントロピーを計算

同様に、 $E_{2}$ を計算すると、

$$
\begin{aligned}
\ E_{4} = &- \sum_{k=1}^{K} t_{k} \log y_{k} &\
&= - ( t_{1} \log y_{1} + t_{2} \log y_{2} + t_{3} \log y_{3}) & \
&= - ( 0 \cdot \log 0.34 + 1 \cdot \log 0.33 + 0 \cdot \log 0.33) \
&= \log 0.34 = -0.46852 \
\end{aligned}
$$

具体的な値を入れてみましょう。さきほどのデータ番号 $i=1$ のデータでみてみましょう。

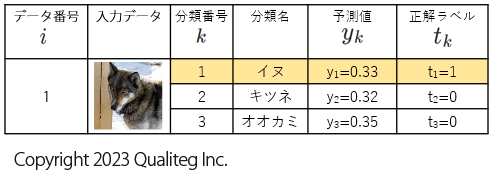
$$
\begin{aligned}
\boldsymbol{E_{1}} = &- \boldsymbol{t} \cdot \log (\boldsymbol{y})& \
=& -
\begin{pmatrix}
t_{1} \ t_{2} \ t_{3}
\end{pmatrix}
\log
\begin{pmatrix}
y_{1} \ y_{2} \ y_{3}
\end{pmatrix}
&
\\
=& -
\begin{pmatrix}
1 \ 0 \ 0
\end{pmatrix}
\log
\begin{pmatrix}
0.33 \ 0.32 \ 0.35
\end{pmatrix}
&
\\
=& -
\begin{pmatrix}
\log(0.33) \ 0 \ 0
\end{pmatrix}
&
\\
=&
\begin{pmatrix}
-0.481486 \ 0 \ 0
\end{pmatrix}
&
\end{aligned}
$$

さて、1件ずつ計算した4件ぶんの交差エントロピー $E_{1}$、$E_{2}$、$E_{3}$、$E_{4}$ を合計したものが、4件ぶんの合計交差エントロピーとなります。これを $E_{sum}$ とすると、

$$
E_{sum} = E_{1} + E_{2} +E_{3} +E_{4}
$$

これを $\sum$ で表現すると、データ番号を $i$ として

$$
E_{sum} = \sum_{i=1}^4 E_{i}
$$

となります。

今はデータ件数が 4件でしたが、これを $N$ 件と一般化すると、

$$
E_{sum} = \sum_{i=1}^N E_{i} \tag{6.1}　
$$

となりますね。

ところで、もともと $t_{k}$ や $y_{k}$ は、分類番号を添え字につけており、今回だと「イヌ」「キツネ」「オオカミ」の3つに分類をしたかったので、 $k={1},k=2,k=3$ としていました。
これは1件ぶんのデータ用としてはこれでよかったのですが、いまは 4件のデータがあるので、 $t_{k}$ と $t_{k}$ を一意に特定できるようにするため、データ番号 $i$ を添え字として追加します。

具体的には以下のように $t_{k}$ → $t_{ik}$ 、 $y_{k}$ → $y_{ik}$ のように拡張しました。

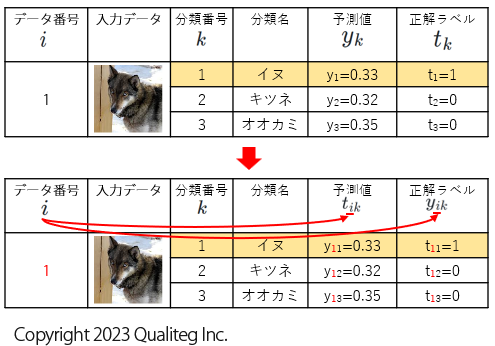
これで、

$t_{ik}$ は訓練データの $i$ 番目のデータの $k$ 番目の要素
$y_{ik}$ は訓練データの $i$ 番目のデータを入力したときのモデルの出力（予測値）の $k$ 番目の要素

という意味となります。

よって $i$ 番目のデータの交差エントロピーは式 $(5.2)$ に添え字 $i$ のを追加した以下のようになります。

$$
E_{i} = - \sum_{k=1}^{K} t_{ik} \log y_{ik} \tag{6.2}
$$

$式(6.1)$ より

$$
\begin{aligned}
E_{sum} =& \sum_{i=1}^N E_{i} &\
\end{aligned}
$$

なので、データ N 件分を合計した交差エントロピーの合計は以下のようになります。

$$
\begin{aligned}
E_{sum} = & - \sum_{i=1}^N \sum_{k=1}^{K} t_{ik} \log y_{ik} &\
\end{aligned}
$$

上式は $N$ 件分の合計値ですが、件数が異なっても比較できるように N で割って交差エントロピー $E_{i}$ の平均をとり、 バッチ版つまり複数データ対応バージョンの交差エントロピー関数 $E$ は以下のように定義されます。

$$
E = - \frac{1}{N} \sum_{i=1}^N \sum_{k=1}^{K} t_{ik} \log y_{ik} \tag{6.3}
$$

$$
\begin{aligned}
\
& N:データ件数& \
&i:データ番号& \
&K:分類の数& \
&k:分類番号& \
&t_{ik}: i 番目のデータの k 番目の正解ラベル(教師データ)& \
&y_{ik}:i 番目の入力データの出力のうち k 番目予測値& \
\end{aligned}
$$

ようやく、冒頭に紹介した多値分類用の交差エントロピー関数が定義できました。これを英語では Categorical Cross Entropy と呼びます

今回はいかがでしたでしょうか

無事、データN件対応版の多値分類用交差エントロピーを導くことができました。
次回は、　二値分類用の交差エントロピーを導いていきたいと思います。

参考文献
https://blog.qualiteg.com/books/

navigation