人気ゲーム「ヒット&ブロー」で学ぶ情報理論

こんにちは!
Qualiteg研究部です!
今日はAIにおいても非常に重要な情報理論について、Nintendo Switchの人気ゲーム「世界のアソビ大全51」にも収録されている「ヒット&ブロー」というゲームを題材に解説いたします!

はじめに
論理的思考力を鍛える定番パズルゲームとして長年親しまれている「ヒット&ブロー」(海外では「Mastermind」として知られています)。
このゲームは一見シンプルながらも、その攻略には深い論理的アプローチが必要とされております。
本稿では、このゲームについて情報理論という数学的概念を用いてゲームの素性を分析する方法について掘り下げてみたいとおもいます。
さらに、この情報理論が現代の人工知能(AI)技術においてどのように活用されているかについても触れていきます。
ヒット&ブローのルール説明
ヒット&ブローは、相手が秘密に設定した色や数字の組み合わせを推測するゲームです。日本では主に数字を使った「数当てゲーム」として親しまれていますが、本記事では色を使ったバージョン(マスターマインド)に焦点を当てます。
Nintendo Switchの「世界のアソビ大全51」で遊べるヒット&ブローでは、6色から4つを選んで並べるルールが採用されており、プレイヤーは最大8ターンの中で正解を導き出す必要があります。
ゲームの基本ルールは以下の通りです。
●6色の玉がある
(本当はピンですが、玉のほうが言いやすいので、玉とよびますね^_^ )

●4つの玉をある順序で並べたものが正解となる
出題者(まぁコンピューターですね)は、たとえば、以下のように6つの玉から4つの玉を抽出し、それをある順序で並べて、それを、あらかじめ正解として決めます。

●挑戦者はその色の組み合わせと配置順序を当てることが目標です。
●挑戦者が色の組み合わせを提示すると、出題者は以下の形式でフィードバックを返します
- 「ヒット」:色も位置も正解である場合
- 「ブロー」:色は正解だが位置が異なる場合
つまり挑戦者が提示した組み合わせを正解の組み合わせと比べると、何個ヒットしたか、何個がブローだったかがフィードバックされます。
このフィードバックだけを頼りに、挑戦者は限られた回数の試行内で正解にたどり着くことを目指します。
通常、10回程度の試行制限が設けられていますが、より効率的な攻略法を用いれば、5〜7回程度で正解を導き出すことが可能です。
このゲームの魅力は、限られた情報から論理的に可能性を絞り込んでいく過程にあります。各試行で得られるフィードバックを最大限に活用し、効率よく正解へと近づいていく戦略が求められます。
また、このゲームは数学的な研究の題材としてもわかりやすいので、その攻略法については過去無数に提案されており、学術論文にもなっていたりします。
さて、せっかくなので、やってみましょう。
ヒット&ブローの攻略法の一例説明
ヒット&ブローには様々な攻略法が存在しますが、ここでは特にNintendo Switchで遊べる6色4ピンのバージョン(8ターン制限)で我が家で実際にプレイしたときの様子を例にちょっとやってみましょう。
◆ 1ターン目チャレンジ
最初は、正解パターンはまったくわからないのでとりあえず、2色ずつ入れてみましょうか。ということで初手は以下のようにしてみました

◆ 1ターン目フィードバック
すると、以下のようなフィードバックがありました。

これは、以下のような意味になります。

オレンジ色の●が1つありましたので、ヒットが1つ
白色の●が1つありましたので、ブローが1つ
というインジケーターです。ヒットは玉の色も位置も正解を示し、ブローは色だけが正解なので、1ターン目で私が提示した玉の組み合わせは1つは位置があっていて、もう1つは色があっているということがわかりました。
●と●のどちらも色は正解、位置はどちらかが正解となるので、そうなると、以下のような場合分けをすることができそうです。
【●がヒット】と仮定すると、上の2つのうちのどちらかが●となり、かつ、もう一方の●も色はあっていることから、上半分は以下のパターンが予想される

【●がヒット】と仮定すると、下の2つのうちのどちらかが●となり、かつ、もう一方の●も色はあっていることから、下半分は以下のパターンが予想される

ということで、案外色々わかりました
◆ 2ターン目チャレンジ
さて、2ターン目にいきましょう。
どんな玉を置きましょうか。
●と●については、まあまあわかったので、今度は別の色の組み合わせにしてみましょう。
また2個ずつ置いてみましょうか。
ということで今度は、まだ使ってない玉の中から選んで
●と●を以下のように置いてみることにしましょう。

◆ 2ターン目フィードバック
すると、以下のようなフィードバックをもらいました。ヒット:0、ブロー:1です。
ゲームの盤面にするとこんな感じです。
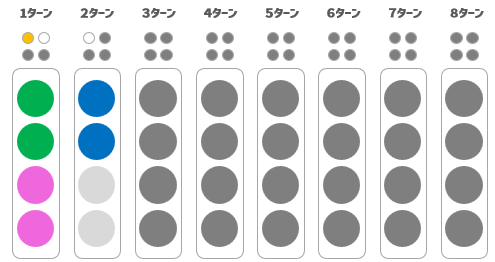
さて、この結果からわかることは、
●または、●は正解色である
ことがわかりますね。
さらに、上記より、いままで選ばれなかった残りの玉については、
●または、●は正解色である
ことも同時にわかりますね。
◆ 3ターン目チャレンジ
さて、3ターン目です。
そろそろターンごとの戦略目標を設定してみましょうか。
この3ターン目の目標は1ターン目と2ターン目で得られた情報のブラッシュアップです。具体的には、
【3ターン目の目標】
・1ターン目のヒットは●だったのか否か を確認
もう1つ、
・2ターン目のブローは●だったのか否か を確認
さあ、この目標を達成するためには、以下のように組み合わせてみるのが良いのではないでしょうか。

上部の2つの●で1ターン目のヒットは●であったのか否かの確認ができます。
下部の2つの●で、2ターン目の●がブローだったのか否かを確認できます。
このとき、ありえるフィードバックについて考えてみると、以下の4つのパターンしか存在せず、かつ、この4つのパターンのどれがでても、今ターンの目標を達成することができそうです
パターン1
ヒット1、ブロー1→●がヒットだった、●がブローだった
パターン2
ヒット1、ブロー0→●がヒットだった、●がブローだった
パターン3
ヒット0、ブロー1→●がヒットだった、●がブローだった
パターン4
ヒット0、ブロー2→●がヒットだった、●がブローだった
◆ 3ターン目フィードバック
さて、頭の整理ができたところでチャレンジを実行してみたところ、以下のようなフィードバックでした
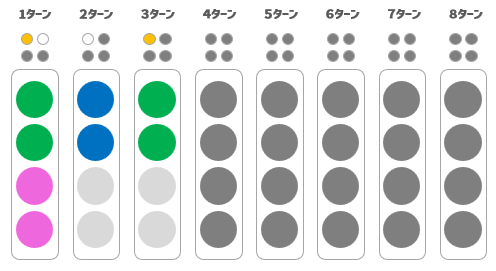
結果はパターン2のヒット1、ブロー0でした
つまり、このことから
●がヒットだった、●がブローだった
ことがわかりました。
まず、
●がヒットだったことがわかったので、
玉の並び順の上二つは、

まで絞り込むことができました。
また、●がブローだったので、●はハズレ玉であることも確定しましたね。
さらに、2ターン目の結果より●が上半分には無いことがわかっていますから、●は下半分に存在することがわかります。

◆ 4ターン目チャレンジ
さて、3ターンを終えていろいろ見えてきましたね。
4ターン目でさらなる追い込みをかけていきましょう。
このターンの戦略目標を決めましょうか。
目標1:上半分の並び順の確定。以下を確定したいですね。

目標2:●の位置の確定。以下のどちらかであるのか、確定したいですね。

目標3:残り1つの玉の色の確定。残り1つの玉は●なのか●なのか
さて、上記目標を達成するための最善手はどうなるでしょう?
おそらく以下ではないでしょうか。

まず上半分で目標1である、●と●の並び順を調査します。
下半分では、残り1色を確定したいとおもいおます。
ここであえて、ハズレ玉●を混ぜている理由は、もし、●が当たり玉だった場合、●の位置も特定できるためです。もし●の位置が特定できるとなると、●の位置も自動的にわかりますね。
この配置にすることで、1/2の確率でこのような幸運に恵まれますね。
さて、じゃあ、はじめから以下のようにやっちゃえばいいじゃんともおもうのですが、こうしてしまうと、もしヒット2がでたとき、上半分が正解なのか、下半分が正解なのかわからないので、あまり筋がよくないかもしれません

◆ 4ターン目フィードバック
ということで結果をみてみまそう。
4ターン目のフィードバックはこうなりました
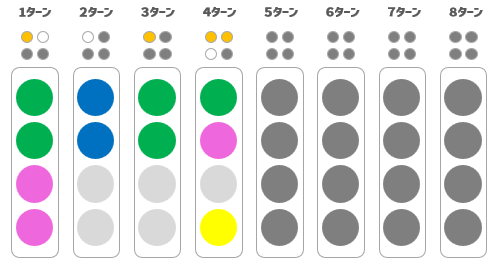
ヒット2、ブロー1
この結果より、わかったことをまとめてみましょう!
①上半分の並び順が確定しました
上から、●と●が正解ですね
②●がブローでしたので、4色が確定し、●●●●であることがわかりました。
③●がブローでしたので、●は上から3番目だとわかりました。
④③より●は一番下に位置するとわかりました
ということで、すべての玉の位置が判明しました!
◆ 5ターン目で勝利
ということで、正解は、

であることがわかりましたので、5ターン目にこれをチャレンジして、
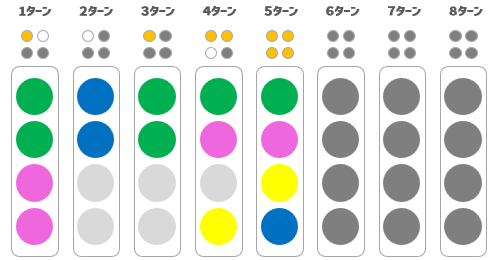
はい!4ヒットで全問正解となりました!
論理的に分析していくことで5ターンで正解を出すことができました。なるべく運の要素をつかわず論理で勝負することを目標に最善手を選んでみたつもりですがいかがでしょうか。
この手法の場合、初手の目により多少の玉選びの差はあるものの5ターン程度で正解にたどり着くことが可能です。Nintendo Switchのヒット&ブローの8ターン制限内でも十分に余裕があるとおもいます。
さて、今回の5ターンというのは本当に良い数字なのでしょうか? じつは3ターンで攻略できるアプローチはあるのではないか?
さて、ここからは、そういった疑問をクリアにすることができる情報理論についてみていきたいとおもいます。
情報理論を応用することで、最小限のターン数を理論的に求めることができます!
情報理論とは何か
情報理論は1940年代にクロード・シャノンによって創始された、情報の定量化と伝達に関する数学的枠組みです。
この理論は当初、電気通信の効率化を目的として開発されましたが、現在では計算機科学、暗号理論、統計学、物理学、そしてAIなど多岐にわたる分野で応用されています。
情報理論の中心概念は「情報量」です。
情報量は不確実性の減少度合いとして定義され、通常はビット(bit)という単位で測定されます。
例えば、公平なコインの表裏を当てるには1ビットの情報量が必要です。なぜなら、表と裏の2つの可能性から1つを特定するためには、log₂(2) = 1ビットの情報が必要だからです。
同様に、6面サイコロの目を当てるには約2.58ビット(log₂(6))の情報が必要になります。このように、選択肢の数をNとすると、その中から1つを特定するために必要な情報量はlog₂(N)ビットとなります。
情報理論のもう一つの重要な概念は「エントロピー」です。
エントロピーは不確実性や情報の混沌度を表す尺度であり、可能な状態のそれぞれの確率に基づいて計算されます。システムのエントロピーが高いほど、そのシステムには多くの不確実性があり、したがって多くの情報が含まれていることになります。
また、「相互情報量」という概念も重要でこれは、ある変数に関する知識が別の変数の不確実性をどれだけ減少させるかを測定するものです。
例えば、ヒット&ブローのゲームでは、各ターンのフィードバックによって得られる相互情報量を最大化するような戦略が理想的です。
このように、情報理論は不確実性を定量化し、情報の伝達効率を最適化するための数学的基盤を提供しています。
情報理論で「ヒット&ブロー」の最善手数を予想してみる
情報理論の視点からヒット&ブローのゲームを分析すると、理論的な最小ターン数を計算することができます。
この分析では、「必要な情報量」と「1ターンで獲得できる最大情報量」という二つの要素が鍵となります。
まず、ゲームの全可能性を考えましょう。
今回やってみた「世界のアソビ大全51」で遊べるヒット&ブローでは6色の玉から4つえらんで順番に並べるヒット&ブローでは、
可能な組み合わせの総数は 6P4 (パーミュテーション6の4ですね)つまり、6個の異なる要素から順番を考慮して4個選ぶ場合の数になりますので
6P4 = 6! ÷ (6-4)! = 6! ÷ 2!
まず階乗を計算します: 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720 2! = 2 × 1 = 2
したがって: 6P4 = 720 ÷ 2 = 360
答えは 360 通りです。
必要な情報量(エントロピー)の算出
この中から正解を一つ特定するために必要な情報量は
360 通りの中から正解を一意に特定するために必要な情報量は、情報理論でのエントロピーとして
log₂(360) ≈ 8.94ビット
となります。
次に、各ターンで獲得できる情報量を考えます。
4ピンのヒット&ブローでは、各ターンのフィードバックとして「ヒット」と「ブロー」の組み合わせが返されます。
世界のアソビ大全のヒット&ブローでは、玉(ピン)の色の重複を許さないルールなので、ヒットとブローのパターンをヒット数とブロー数の合計値でまとめると (ヒット数、ブロー数)とすると
- 合計が2のとき: (2,0), (1,1), (0,2) 【3通り】
- 合計が3のとき: (3,0), (2,1), (1,2), (0,3) 【4通り】
- 合計が4のとき: (4,0), (2,2), (1,3), (0,4) 【4通り】
の全部で11通りです。
情報理論では,ある事象が n 個の等確率なアウトカムに分割されるとき,その情報量は
log2(n)ビットとなるため、1ターンで得られる最大情報量は log₂(11) ≈ 3.46ビットとなります。
理論上の最小ターン数を計算すると、必要情報量÷1ターンの最大情報量 = 8.49÷3.46 ≈ 2.45となります。小数点を切り上げると、理想的な状況では3ターンで解ける計算になります。
ただし、実際のゲームプレイでは、以下の理由により理論値よりも多くのターンが必要になります
- 毎回の試行で最大情報量を獲得できるとは限りません。特に初期のターンでは、情報が不足しているため最適な選択が難しい
- 人間が実行できる現実的な戦略には限界がある。つまり、人間のプレイヤーには認知的な制約がある(コンピューターのように全可能性をしらみつぶしに計算するのは人間の脳みそには厳しい)
- 運の要素も無視できない
最初の推測が偶然多くの情報をもたらすこともあれば、ほとんど情報が得られないこともある
これらの要因を考慮すると、実際の最適プレイでは
- 平均的には:5ターン前後
- 最悪ケースでは:6-7ターン
という見積もりが妥当ではないでしょうか、
ということで、私の考えた攻略法も、まぁ、そう悪くはない、ってことにしておきたいとおもいます。^o^
さて、情報理論的アプローチのさらなる応用として、各ターンで「情報量を最大化する選択」を行うという戦略があります。
これは、各ターンで残っている可能性の集合を最も均等に分割するような選択を行うことで、得られる情報量を最大化する方法です。コンピュータプログラムをつかえばこのような最適戦略を実行すると、理論値に近い平均ターン数で解くことも可能となります。
情報理論はAIでも非常に重要な概念
情報理論は現代の人工知能技術において基礎となる概念の一つです。
当社の研究開発でも頻繁に情報理論を活用しています。
情報理論は、その応用範囲がとても広大で、機械学習のアルゴリズム設計から、ニューラルネットワークの訓練方法、さらには自然言語処理に至るまで多岐にわたります。
まず、機械学習の基本的な目標である「データからのパターン抽出」は本質的には情報理論の問題です。
学習プロセスは、データ内の不確実性(エントロピー)を減少させ、有用な情報を抽出する作業と言えます。
例えば、決定木アルゴリズムでは、各分岐点において情報利得(情報エントロピーの減少量)を最大化するような特徴を選択します。
深層学習においては、損失関数として広く使われる「交差エントロピー」は情報理論に直接由来しています。これは、モデルの予測確率分布と真の確率分布の間の差異を測定するための指標です。
(交差エントロピーについては機械学習において非常に重要な理論ですので https://blog.qualiteg.com/cross-entropy-01/ で詳細に解説していますので、ご覧ください。)
また、過学習を防ぐための「情報ボトルネック理論」も、情報理論の応用例の一つです。これは、入力データから関連する情報だけを抽出し、ノイズや無関係な情報を排除することで、より汎用性の高いモデルを構築するアプローチです。
自然言語処理の分野では、言語モデルの評価指標として「パープレキシティ」が用いられますが、これは条件付きエントロピーに基づいています。また、単語の重要性を測る「TF-IDF」スコアも、情報理論の考え方が基になっています。
強化学習においては、「最大エントロピー強化学習」という手法があります。これは、エージェントの行動選択において、目標達成への効率性と探索の多様性のバランスを取るために、エントロピーを制御する手法です。
また、大規模言語モデル(LLM)の世界では、生成テキストの多様性を制御する「温度」パラメータの概念も、確率分布のエントロピーに関連しています。温度を高くすると確率分布が平坦になり(高エントロピー)、より多様な出力が生成されます。逆に温度を低くすると、確率分布が尖り(低エントロピー)、より確実性の高い出力が生成されます。
このように、情報理論はAI技術の様々な側面に深く関わっています。不確実性の定量化、情報の効率的な表現と処理、最適な決定方法の設計など、情報理論の概念はAI研究においても重要なベースとなっています!
まとめ
本稿では、ヒット&ブロー(マスターマインド)というクラシックなパズルゲームを題材に、論理的な攻略法の一例の紹介と、そもそもそういったゲームの素性をはかることのできる情報理論の応用について探求してきました。
今回の攻略法は「分割統治法」の一種と考えることができ、問題全体をいくつかの部分問題に分割(Divide)し、各部分問題を個別に解決(Conquer)して、全体の解を導く戦略で早ければ5ターンで正解にたどり着くことができます。このあたりをさらに探求したい場合には、Knuthのアルゴリズムなどが有名ですので調べてみると面白いとおもいます。
後半はこれを情報理論で解釈してみました。
情報理論における情報量やエントロピーといった概念は、不確実性を定量化し、情報の伝達効率を最適化するための数学的基盤となっており、これらの概念は、現代のAI技術においても広く応用されています。機械学習アルゴリズムの設計から、深層学習の訓練方法、自然言語処理に至るまで多岐にわたる分野で重要な役割を果たしています。
情報理論を用いるとヒット&ブローの最適ターン数はの6色4ピン・重複無しのゲームでは、理論上は3ターンで解ける可能性がありますが、実際には様々な制約から4〜6ターンが現実的な見積もりとなりましたね。
このように、一見単純なゲームの攻略法を通じて、情報理論という深遠な数学的概念がすこし身近になったのではないでしょうか。
情報理論の考え方は、ゲーム攻略だけでなく、日常生活における意思決定や問題解決にも応用できる普遍的な概念なので不確実性を定量化し、最適な情報収集と判断を行うという視点は、多くの場面で役立ちそうですね。
最後までお読みいただきありがとうございました!
また次回お会いしましょう!




