AI数理

スライドパズルを解くAIから学ぶ、「考える」の正体

Qualiteg 研究部

2026年2月12日 — 18 min read

こんにちは！

「このパズル、AIの教科書に載ってるらしいよ」

子供の頃に遊んだスライドパズル。いや、大人が遊んでも楽しいです。

数字のタイルをカチャカチャ動かして揃えるあれです。実はこのシンプルなパズルが、AI研究の出発点のひとつだったって知ってました？

今回は、このパズルを題材に「AIがどうやって考えているのか」を解き明かしていきます。しかも、ここで使われている手法は、Google Mapsの経路探索からChatGPTまで、現代の様々な技術のベースになっているんです。

まず遊んでみよう

理屈の前に、まずは感覚を思い出してみてください。

最初に shuffle をクリックすると、配置がシャッフルされゲームを開始できます。

ちなみに必ず解くことができるようになっていますが、慣れていないとそれなりに難しいかもしれません。

どうでしょう？

何手でクリアできましたか？

クリアできなくても大丈夫です。記事後半で、実際にAIが解いてくれる機能つきゲームも掲載しています＾＾

以下は動画です。本ブログで紹介するアルゴリズムで実際にパズルを解く様子をご覧いただけます

0:00

/0:17

記事後半では、こんな風に、実際にアルゴリズムを実装しています

解いているとき、何を考えていました？おそらく「なんとなく」「端から順番に」「パターンで覚えてる」といった感じではないでしょうか。

実は、この「なんとなく」の正体を数学的に解き明かしたのが、AI研究の出発点のひとつだったんです。

人間はどう解いているのか

人間がパズルを解くとき、だいたいこんなことをしています。

これは非常に「局所的」なアプローチですよね。全体の最短経路を計算しているわけではなく、目の前の問題を一つずつ解決している。人間の脳はこういった直感的な処理が得意で、それなりにうまく解けます。

では、コンピュータはどうアプローチするのでしょうか？

AIの見方：世界を「状態」で捉える

コンピュータは15パズルをこう捉えます。

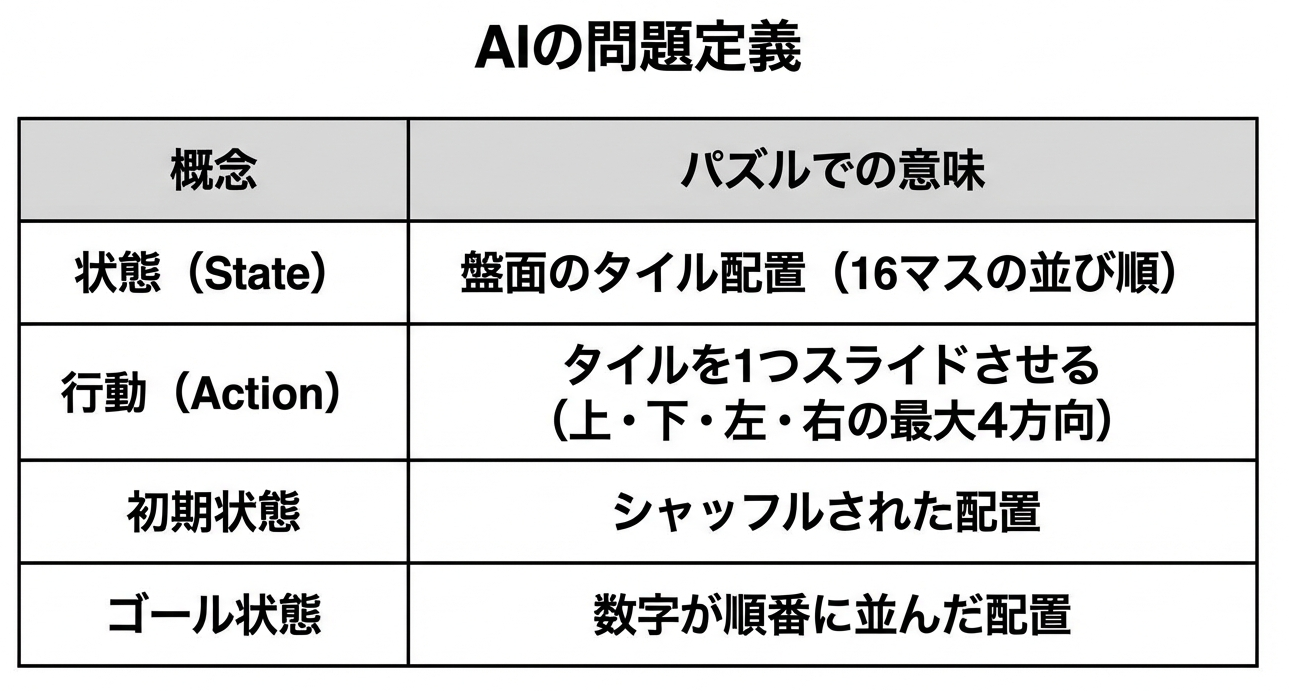
なぜ「状態」で考えるのか？

ここで重要なのは、問題を「状態の遷移」として捉え直すという発想です。

人間は「タイルを動かす」と考えますが、
コンピュータは「ある配置から別の配置に移る」と考えます。

この視点の転換がなぜ重要かというと、問題がグラフ理論の枠組みで扱えるようになるからです。

グラフ理論とは、点（ノード）と線（エッジ）の関係を研究する数学の分野です。パズルの各配置を「点」、1手で移動できる関係を「線」と見なせば、パズルを解くことは「スタート地点からゴール地点への経路を見つける」という、数学的によく研究された問題に変換できます。

つまり、過去何十年にもわたって蓄積されてきた経路探索のアルゴリズムが、そのまま使えるようになるわけです。これが「状態空間探索」というアプローチの強みです。

状態空間の構造

これを図で表すと、状態が枝分かれしていく「木」のような構造になります。

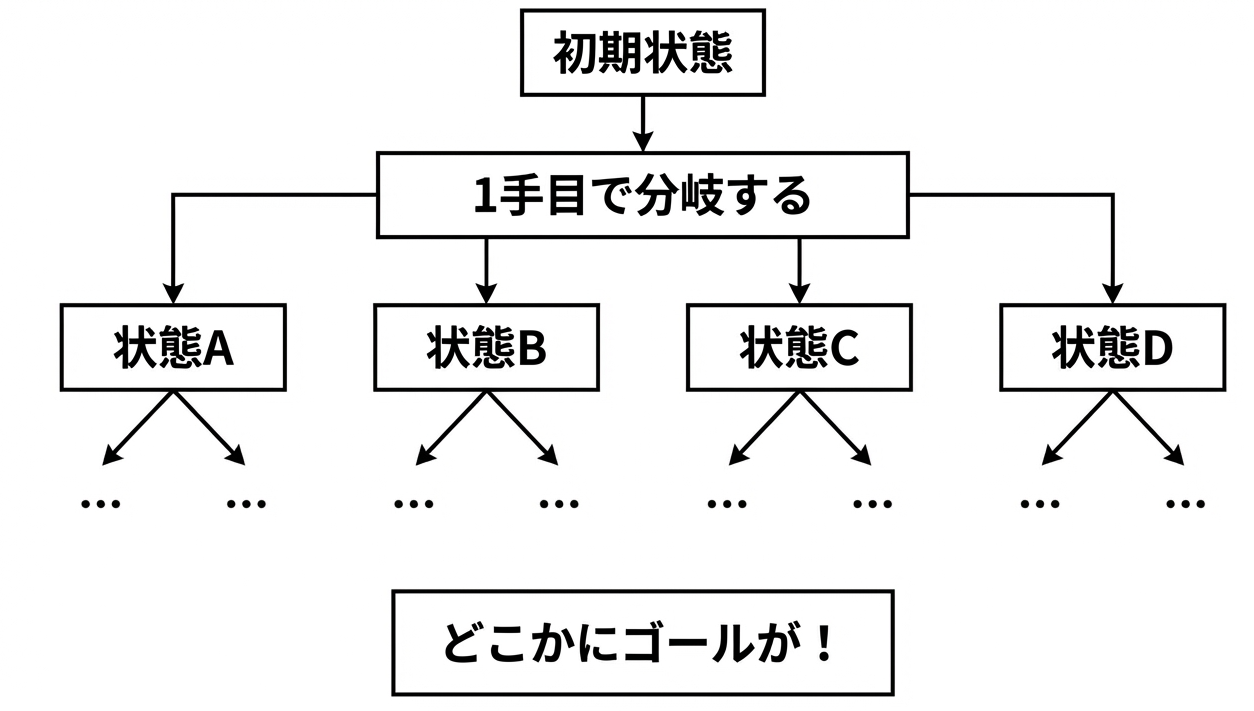
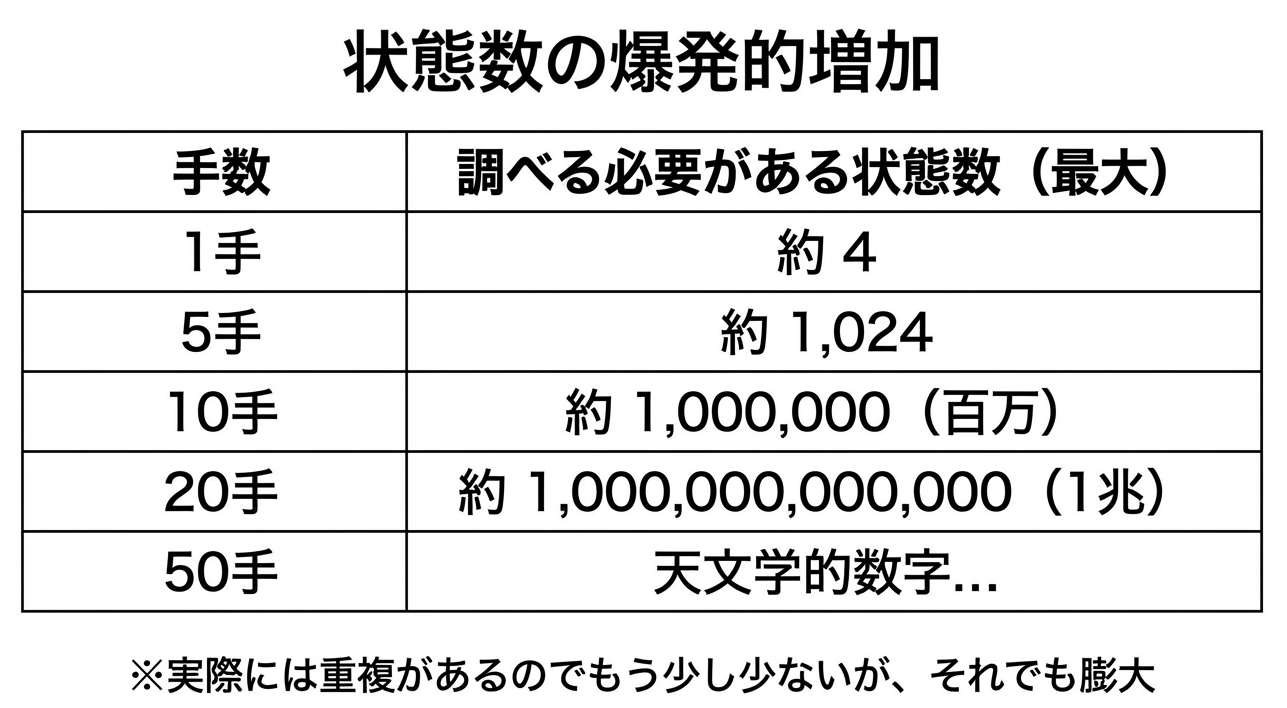
1手で約2〜4通りの状態に分岐します。2手で最大16通り、3手で最大64通り...と、可能性が指数的に広がっていきます。

この「状態の木」のどこかにゴールがあります。コンピュータの仕事は、その経路を見つけることなんです。

ここで「指数的に増える」という表現が出てきました。これは「手数が1増えるごとに、調べる状態が何倍にもなる」という意味です。たとえば毎手4倍になるとすると、10手で約100万、20手で約1兆になります。この爆発的な増加が、パズルを解く難しさの本質です。

解けない配置が存在する！？

ここで面白い事実を紹介しましょう。

15パズルには、どれだけ頑張っても絶対に解けない配置が存在します。

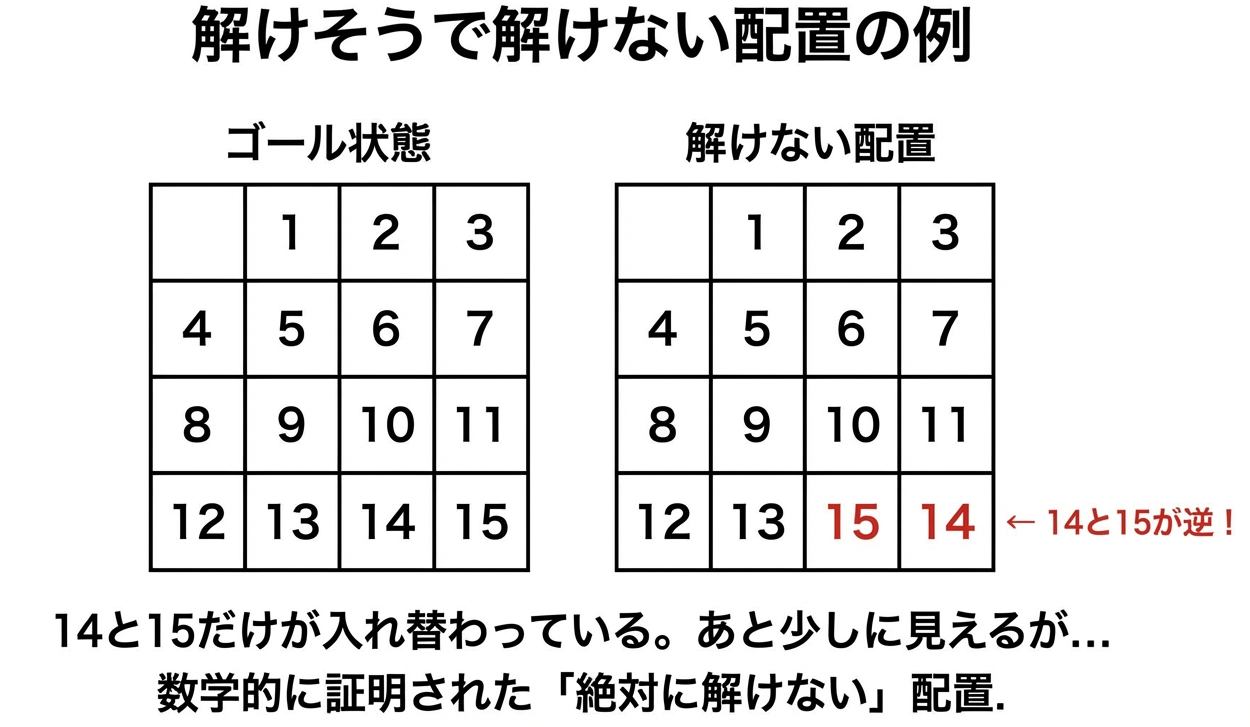
これは1880年代にアメリカで大流行したパズルで、

「解けたら賞金！」

という懸賞が出されたんですが、誰も解けませんでした。後に数学者が「そもそも解が存在しない」ことを証明して決着がついたという歴史があります。

なぜ解けないのか：転倒数（Inversion Count）

判定方法は「転倒数」という概念を使います。

転倒数とは、タイルを順番に見ていったとき、「後ろにあるべき数字が前にある」ペアの数のことです。

なぜ転倒数で判定できるのか？

これは少し数学的な話になりますが、直感的に説明してみましょう。

タイルを1回スライドさせると、転倒数は必ず奇数個だけ変化します（1増えるか、1減るか、あるいは±3など）。つまり、転倒数の「偶奇」（偶数か奇数か）は、1手ごとに必ず入れ替わります。

ゴール状態の転倒数は0（偶数）です。ということは、偶数回の操作でしか到達できません。もし初期状態の転倒数が奇数なら、何回操作しても偶数にはならないので、ゴールには絶対に到達できないってことになりますよね。

これは「不変量（invariant）」と呼ばれる考え方で、システムがどう変化しても保存される性質を見つけることで、到達可能性を判定できます。

今回作ったゲームも、裏側でこの判定を行い、必ず解ける配置だけを生成しています。プログラムで「解けない問題を出さない」ようにしているわけですね。

力任せ vs 賢く探す

さて、解ける配置だとわかったら、どうやって解を見つけるでしょうか。

幅優先探索（BFS: Breadth-First Search）：全部試す方法

最も単純な方法は「幅優先探索」です。

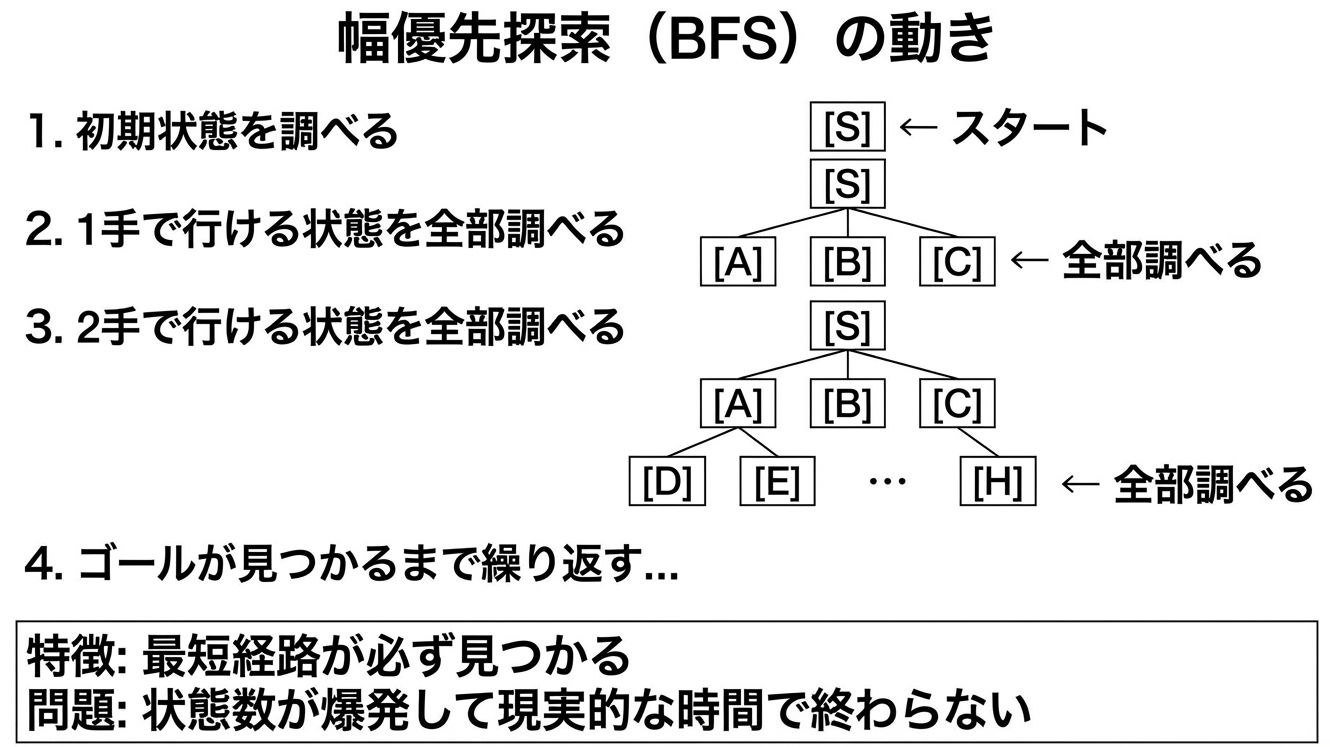
BFSのアルゴリズム

BFSの動きをもう少し詳しく説明しましょう。

BFSは「近い順に全部調べる」という戦略です。まず1手で行けるところを全部調べ、次に2手で行けるところを全部調べ...と、距離（手数）の近い順に探索を進めます。

この方法の最大の利点は、最短経路が保証されることです。なぜなら、5手で到達できる状態は、必ず4手以下の状態をすべて調べた後に見つかるからです。つまり、ゴールを最初に見つけた瞬間、それが最短経路だと確定します。

しかし、この「全部調べる」というのが曲者です。15パズルの場合、20手先まで調べようとすると、約1兆個の状態を調べる必要があります。1秒間に100万個の状態を調べられるコンピュータでも、約12日かかる計算です。

これでは実用的ではありませんよね。。

A*探索（A-star Search）：賢い勘を使う

ここで登場するのが「A*（エースター）探索」です。1968年にスタンフォード大学のPeter Hart、Nils Nilsson、Bertram Raphaelによって発明されたこのアルゴリズムは、「賢い勘」を使って探索範囲を絞り込みます。

A*の基本アイデア

BFSは「手数の少ない順」に探索しました。A*は、これを「ゴールに早く着きそうな順」に変えます。

「ゴールに早く着きそう」かどうかを判断するために、A*は2つの情報を組み合わせます。

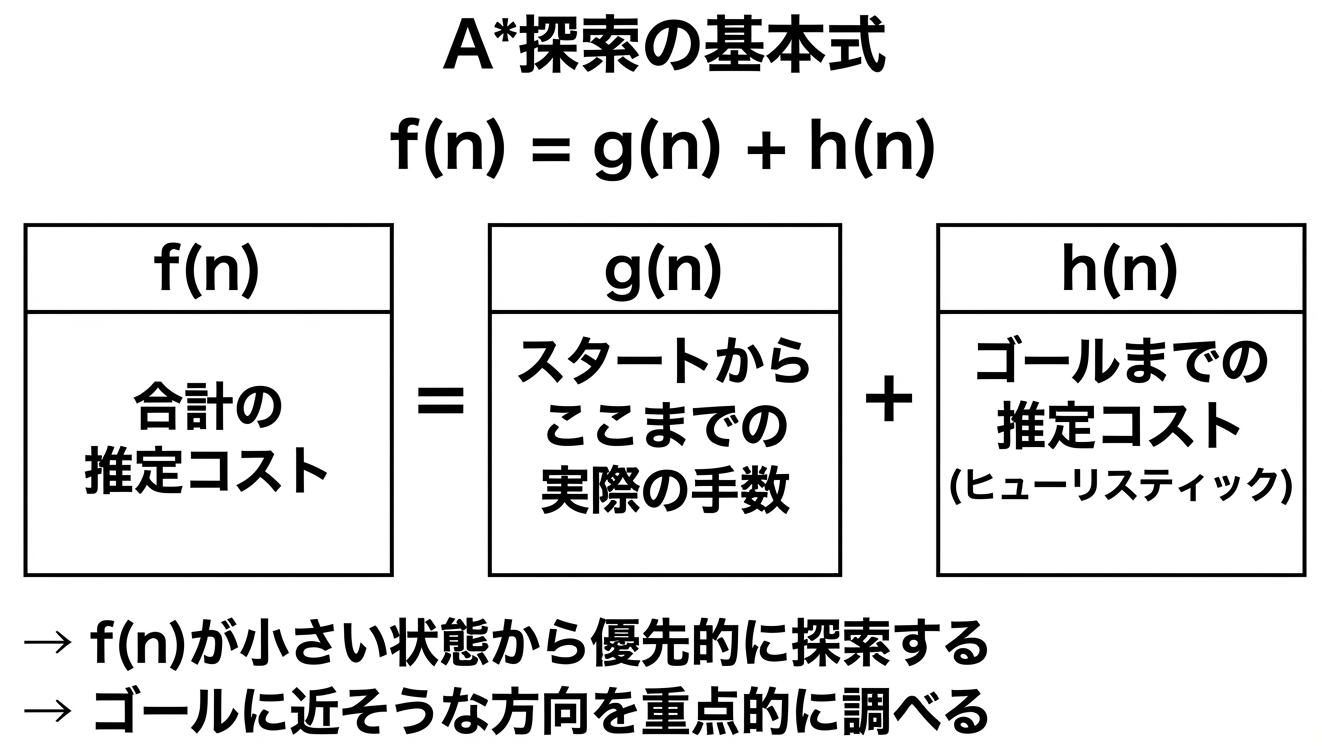
g(n): スタートからここまで実際に何手かかったか（確定値）
h(n): ここからゴールまであと何手くらいかかりそうか（推定値）
f(n): 合計すると、この経路でゴールまで何手くらいかかりそうか

A*は、この f(n) が小さい状態から優先的に探索します。つまり、「全体として手数が少なく済みそうな方向」を優先するわけです。

なぜこれが賢いのか？

BFSが「円形に広がる波」だとすると、A*は「ゴールに向かって伸びる楕円」のようなイメージです。

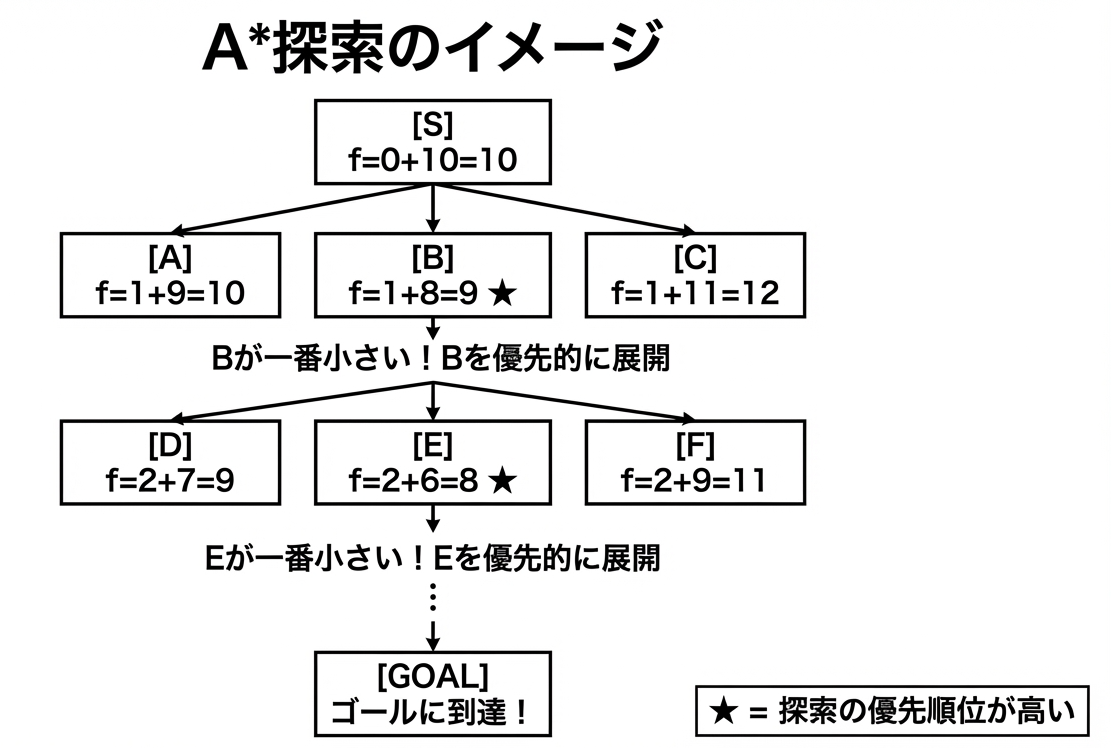
この例では、状態Bの f(n) が9で最小なので、Bを優先的に展開します。AやCは後回しです。もしBの先にゴールがあれば、AやCは調べずに済みます。

これがA*の「賢さ」の本質です。ゴールに近そうな方向を先に調べることで、無駄な探索を大幅にカットできるのです。

ヒューリスティック関数：「勘」を数値化する

A*の性能は、h(n) をどう計算するかにかかっています。この h(n) を計算する関数を「ヒューリスティック関数」と呼びます。

「ヒューリスティック（heuristic）」とは、「発見的な」「経験則に基づく」という意味です。

最適解を保証するわけではないが、多くの場合うまくいく「賢い推測」のことです。

良いヒューリスティックの条件

ヒューリスティック関数には、重要な条件があります。

計算が速いこと: 何百万回も計算するので、1回の計算に時間がかかると台無しです
ゴールに近いほど小さい値を返すこと: そうでないと優先順位が正しくつけられません
許容的（Admissible）であること: 実際のコストを過大評価しないこと

特に3つ目の「許容的」という性質が重要です。これについては後で詳しく説明します。

マンハッタン距離：15パズルの「勘」

15パズルでよく使われるヒューリスティック関数が「マンハッタン距離」です。

マンハッタン距離とは？

マンハッタン距離は、碁盤の目状の道を歩くときの距離です。

ニューヨークのマンハッタン島は道路が格子状になっているので、斜めには歩けません。この「縦か横にしか進めない」ときの距離がマンハッタン距離です。

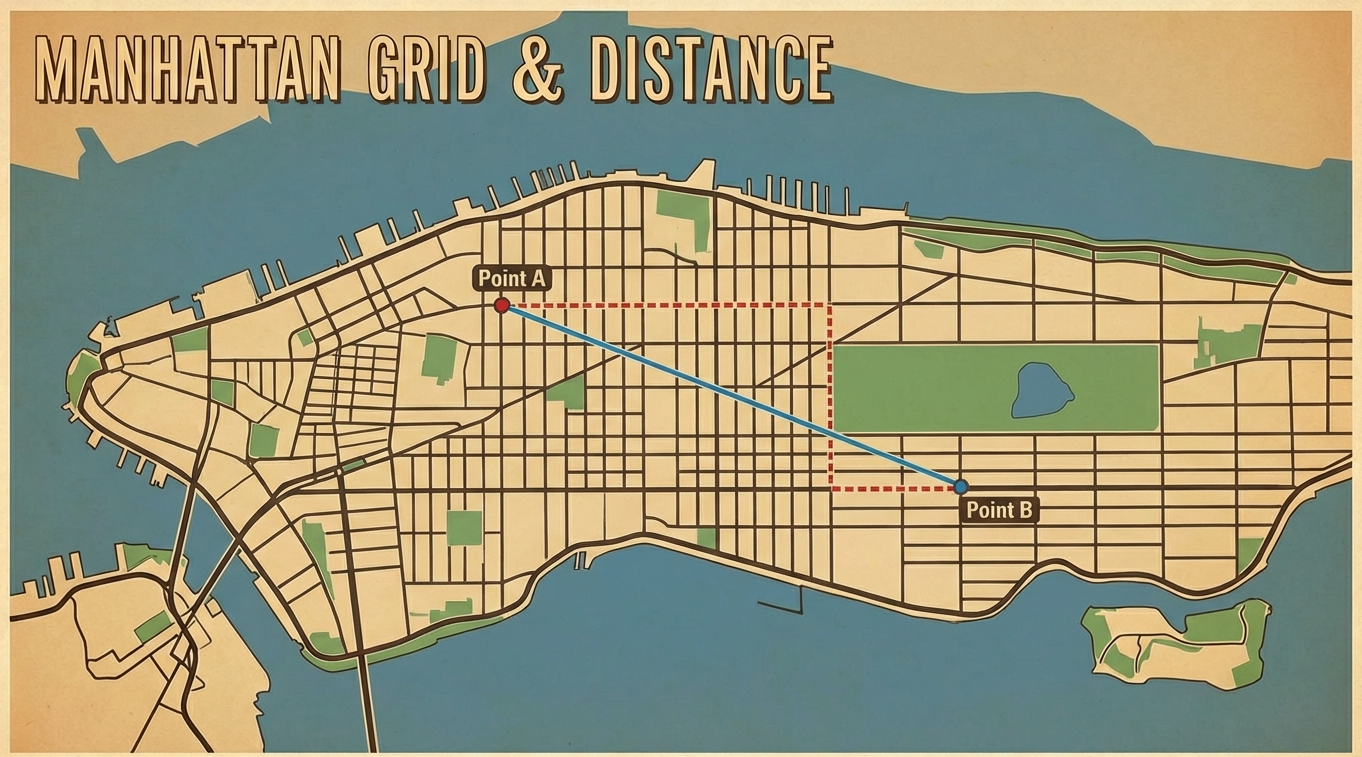
マンハッタン島は道路が格子状。縦か横にしか進めないところから生まれたマンハッタン距離

通常の直線距離（ユークリッド距離）と比較してみましょう。

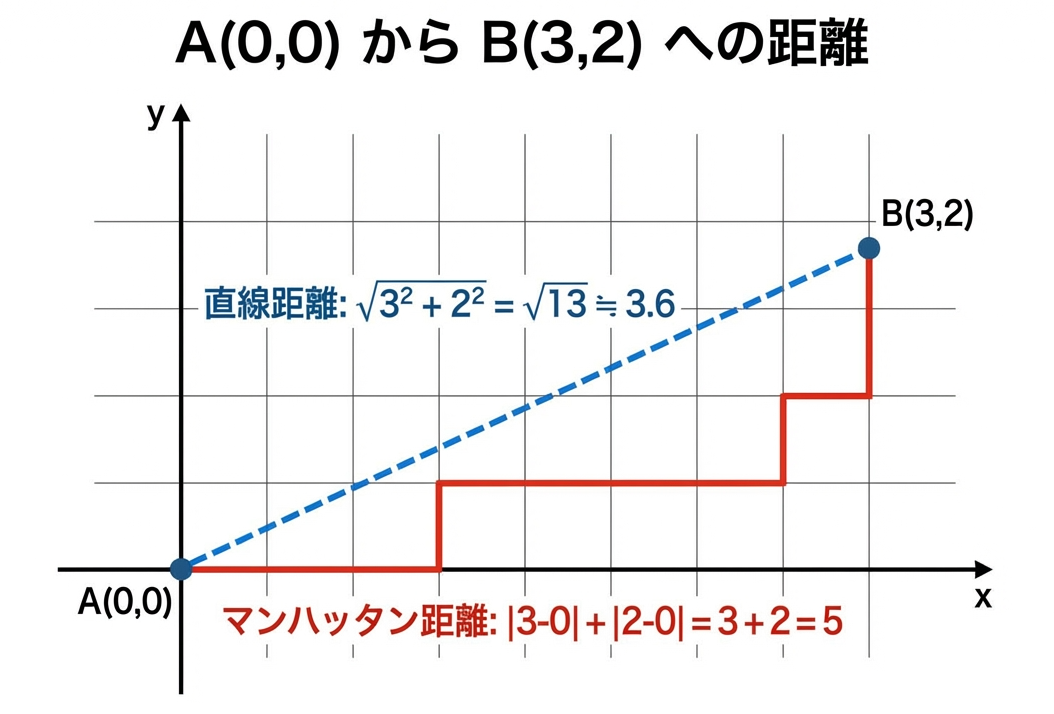
15パズルでは、タイルは上下左右にしか動けないので、マンハッタン距離がぴったり当てはまります。

15パズルでの計算方法

各タイルについて、「今いる場所」と「あるべき場所」のマンハッタン距離を計算し、全部足し合わせます。

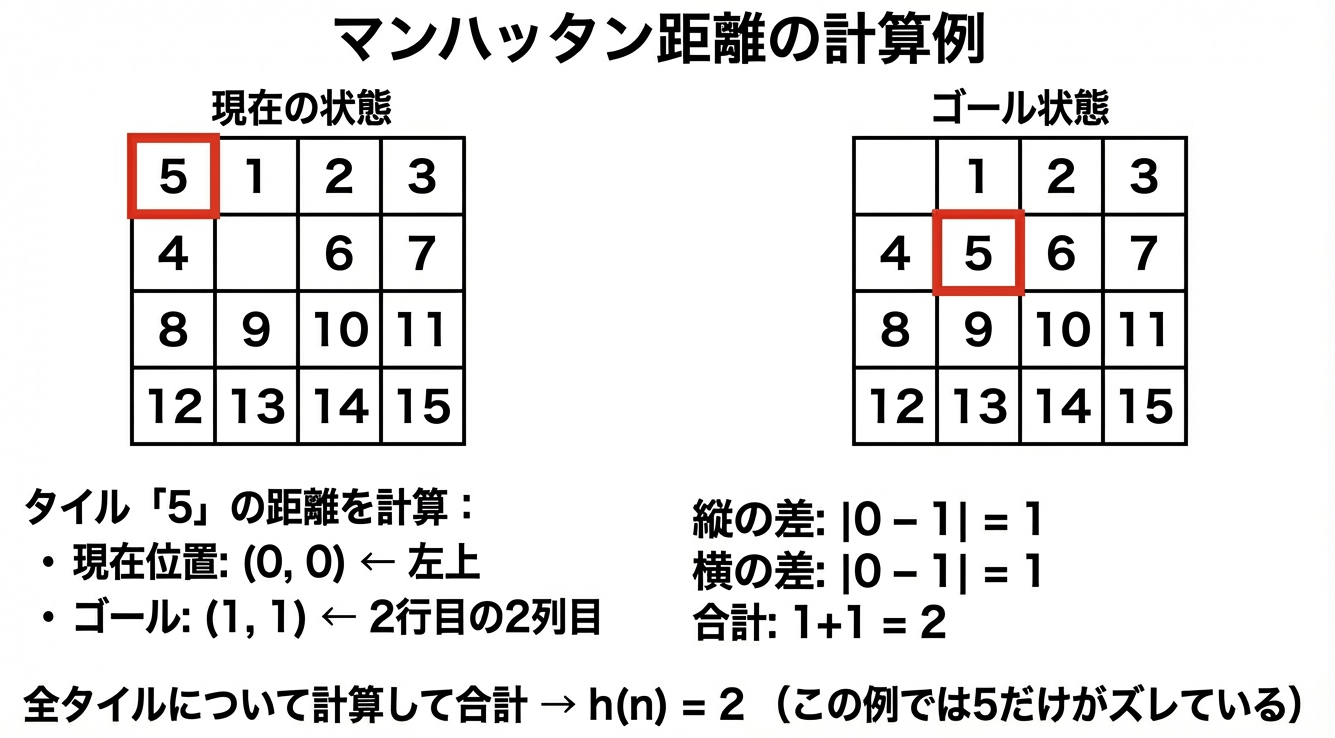
なぜマンハッタン距離が優れているのか？

マンハッタン距離が15パズルに適している理由は3つあります。

計算が高速: 各タイルの座標を引き算して足すだけなので、一瞬で計算できます
直感的に正しい: タイル5が2マス離れていたら、最低でも2回は動かさないと正しい位置に置けません。これは当たり前ですよね
許容的である: ここが重要です。マンハッタン距離は「最低でもこれだけは必要」という下限を示します。実際には他のタイルが邪魔になってもっと手数がかかることが多いですが、過大評価することは絶対にありません

許容的（Admissible）であることの重要性

ヒューリスティック関数が「許容的」であるとは、実際のコストを過大評価しないことを意味します。

なぜ過大評価してはいけないのか？

もし h(n) が実際のコストより大きい値を返すと、「この経路はコストが高そうだ」と誤解して、本当は最短の経路を後回しにしてしまう可能性があります。その結果、最短ではない経路を「最短だ」と誤って返してしまうことがあるのです。

逆に、過小評価する分には問題ありません。「この経路は短そうだ」と思って優先的に調べても、実際に長ければ後から正しい経路が見つかります。

つまり、ヒューリスティック関数は楽観的であるべきなのです。「最低でもこれくらいはかかるだろう」という下限を示すのが正しい使い方です。

マンハッタン距離は許容的

マンハッタン距離は、まさにこの「下限」を示しています。タイル5が位置(0,0)から位置(1,1)に移動するには、最低でも2回の移動が必要です。他のタイルが邪魔をして迂回が必要になることはあっても、2回より少なく移動することは物理的に不可能です。

だから、マンハッタン距離は常に「実際のコスト以下」であり、許容的なんです。

計算量の劇的な違い

実際にどれくらい違うのか見てみましょう。

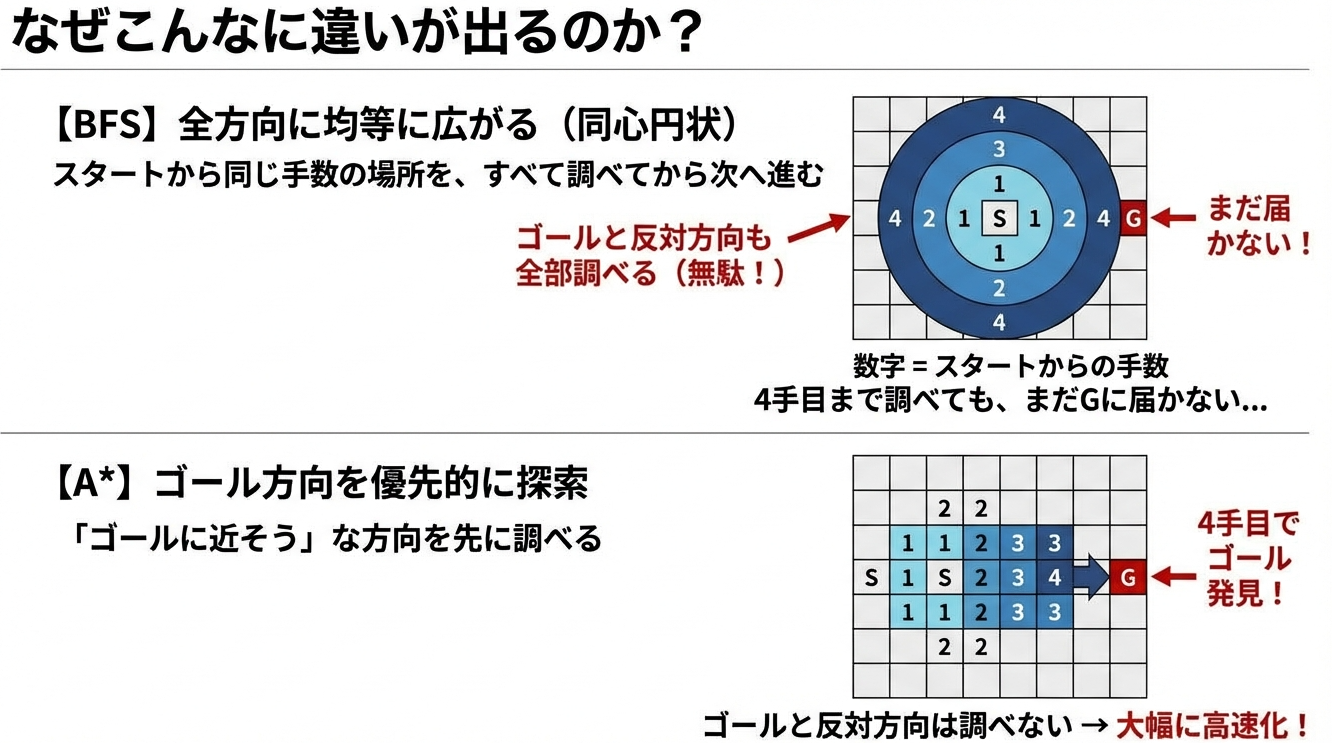
この図が示すように、BFSは「全方向に均等に広がる円」のように探索しますが、A*は「ゴールに向かって伸びる楕円」のように探索します。ゴールと反対方向の無駄な探索を大幅にカットできるので、これほどの差が生まれるんです。

この手法、どんな技術に使われている？

ここからが本題です。15パズルで使った「状態空間探索」「ヒューリスティック」という手法は、現代の様々なAI技術の基盤になっています。

「AI」とひとくちに言っても、ディープラーニング、機械学習、ルールベースなど様々な技術があります。今回のパズルで使った手法は、どこに位置するのでしょうか？

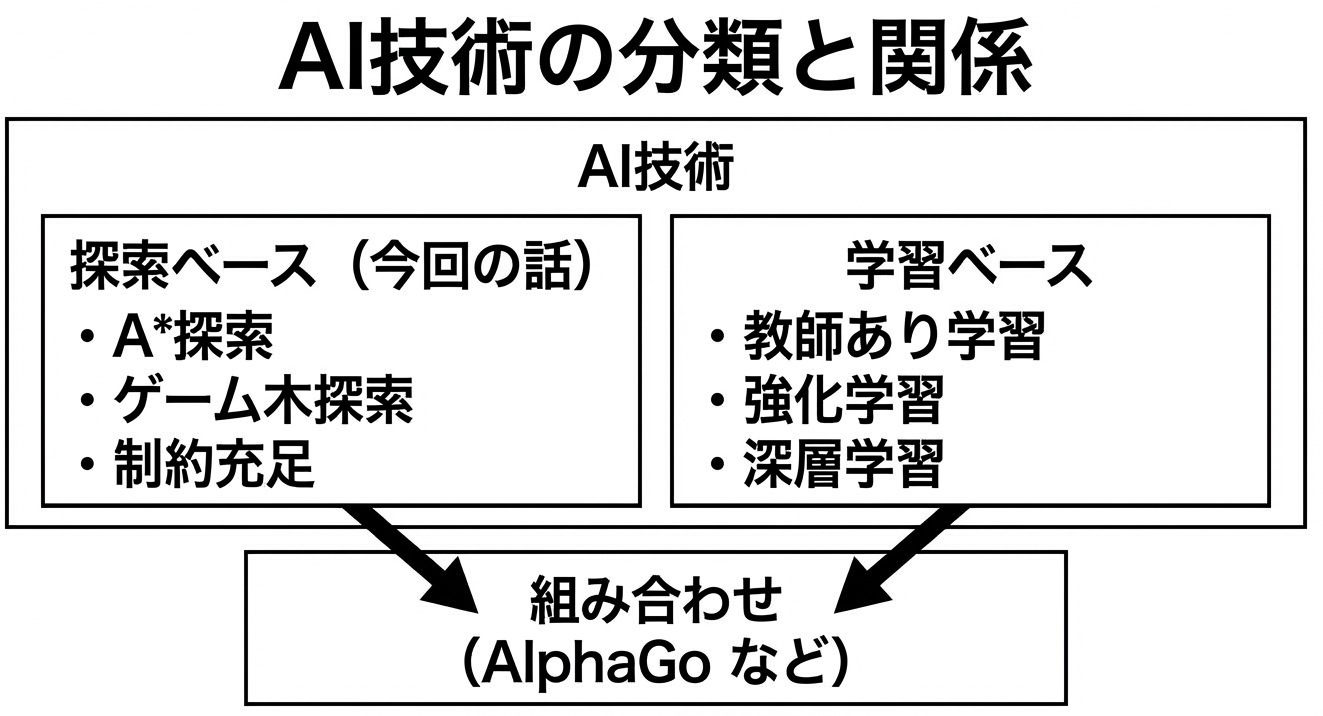
探索ベース vs 学習ベース

AI技術は大きく「探索ベース」と「学習ベース」に分けられます。

探索ベースは、問題の構造が明確に定義できる場合に使います。状態、行動、ゴールが明確で、「正解への道筋を探す」という形式で問題を解きます。今回の15パズル、チェス、経路探索などがこれに当たります。

学習ベースは、大量のデータから「パターン」を学ぶアプローチです。画像認識、音声認識、推薦システムなど、ルールを明示的に書くのが難しい問題に向いています。ディープラーニングやランダムフォレストはこちらに分類されます。

そして現代の最先端のAI（AlphaGoなど）は、両者を組み合わせています。探索の「賢い推定」を、学習によって獲得します。

具体的な応用先

それぞれ詳しく見ていきましょう。

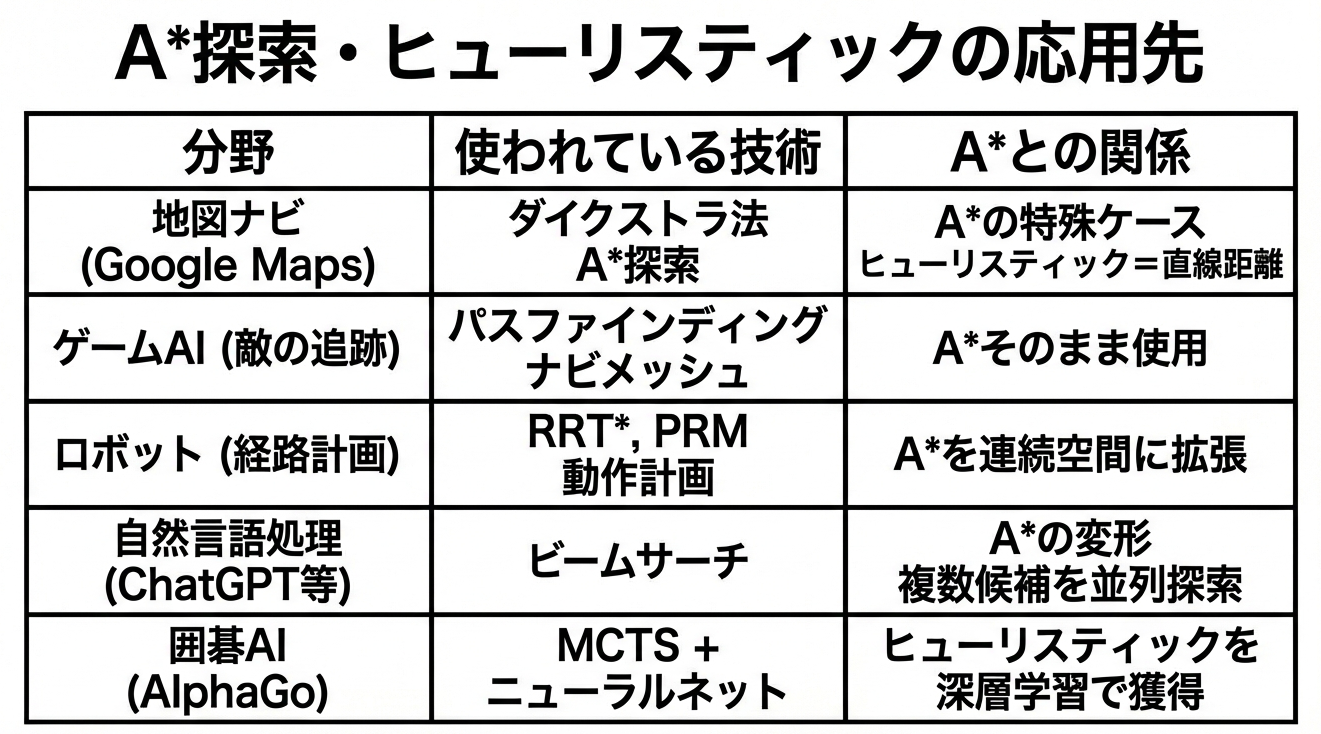
1. Google Maps の経路探索

カーナビやスマホの地図アプリが一瞬で経路を出せるのは、A*探索のおかげです。

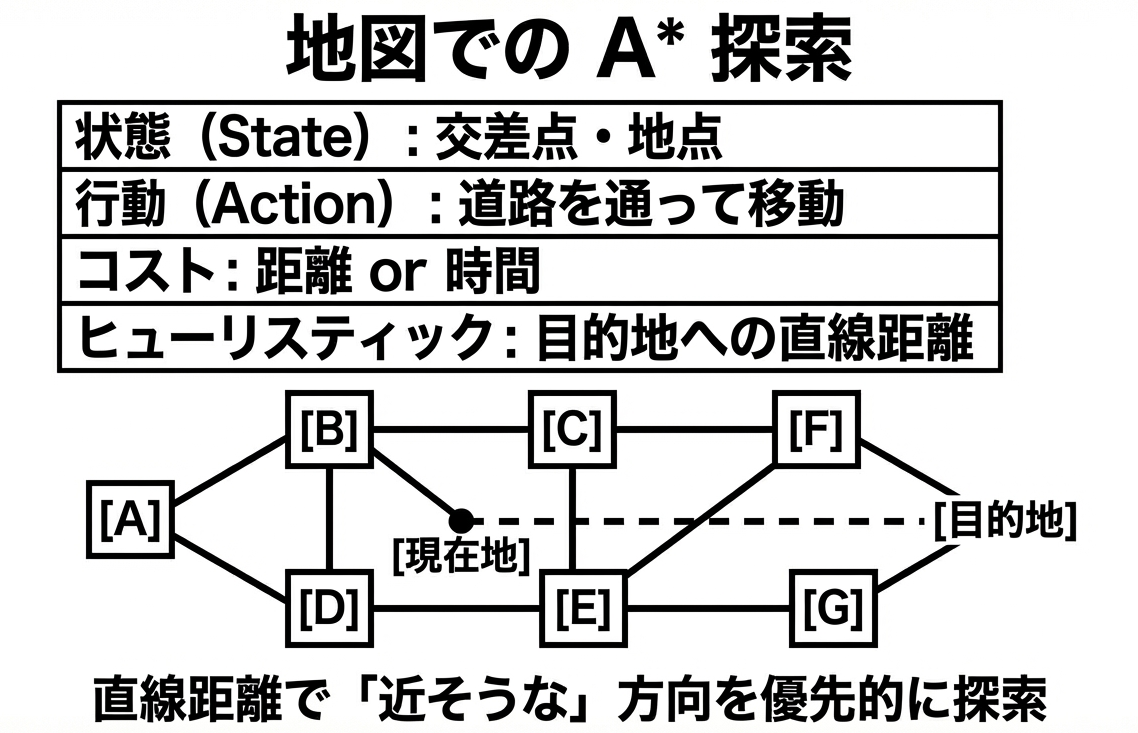
地図の場合、ヒューリスティック関数は「目的地への直線距離」です。道路は曲がりくねっていますが、直線距離より短くなることはありません。だから許容的です。

実際のGoogle Mapsはさらに高度な最適化（階層的な探索、事前計算など）を行っていますが、基本的な考え方はA*と同じです。

2. ゲームAI（パスファインディング）

RPGやアクションゲームで、敵キャラクターがプレイヤーを追いかけてくる動き。障害物を避けながら最短経路で近づいてきますよね。これもA*探索です。

ゲーム開発では「パスファインディング」と呼ばれ、UnityやUnreal Engineにも標準で組み込まれています。

3. ロボットの動作計画

ロボットアームがものを掴んで別の場所に置く。この動きを計画するのにも、状態空間探索が使われます。

ロボットの場合、「状態」は関節の角度の組み合わせです。6軸のロボットアームなら、6つの角度を指定すると手先の位置が決まります。「行動」は各関節を少し動かすこと。「ゴール」は目標の位置に手先を持っていくことです。

ただし、ロボットの状態空間は連続的（角度は実数）なので、15パズルのような離散的な問題とは少し違います。RRT*（Rapidly-exploring Random Tree*）やPRM（Probabilistic Roadmap）といった、連続空間に対応したアルゴリズムが使われますが、「ゴールに近そうな方向を優先する」という基本的な考え方は同じです。

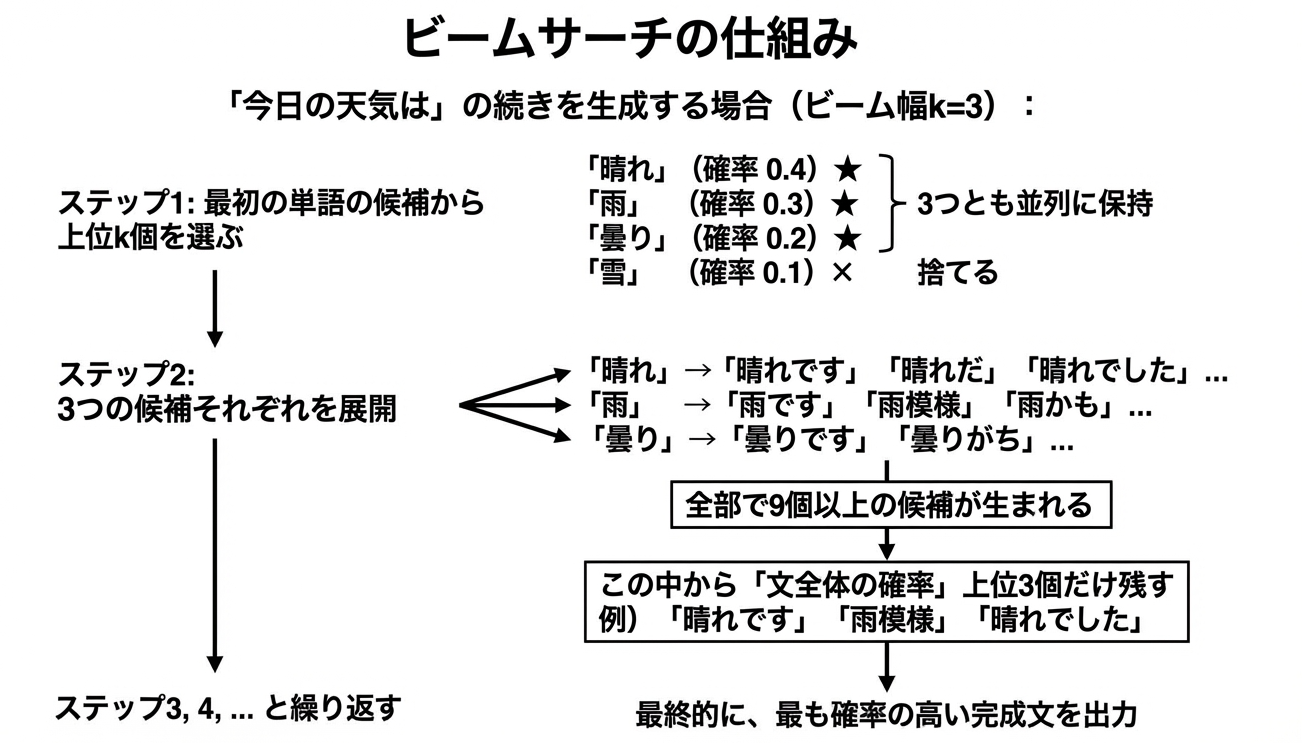
4. ChatGPTなどの言語モデル（ビームサーチ）

ここが面白いところです。ChatGPTのような大規模言語モデル（LLM）が文章を生成するとき、「次にどの単語を選ぶか」を決める過程でビームサーチという手法が使われることがあります。

top-k サンプリングとの違い

ここでLLMかいわいで有名な「top-k」という似た用語があるので、違いを整理しておきましょう。

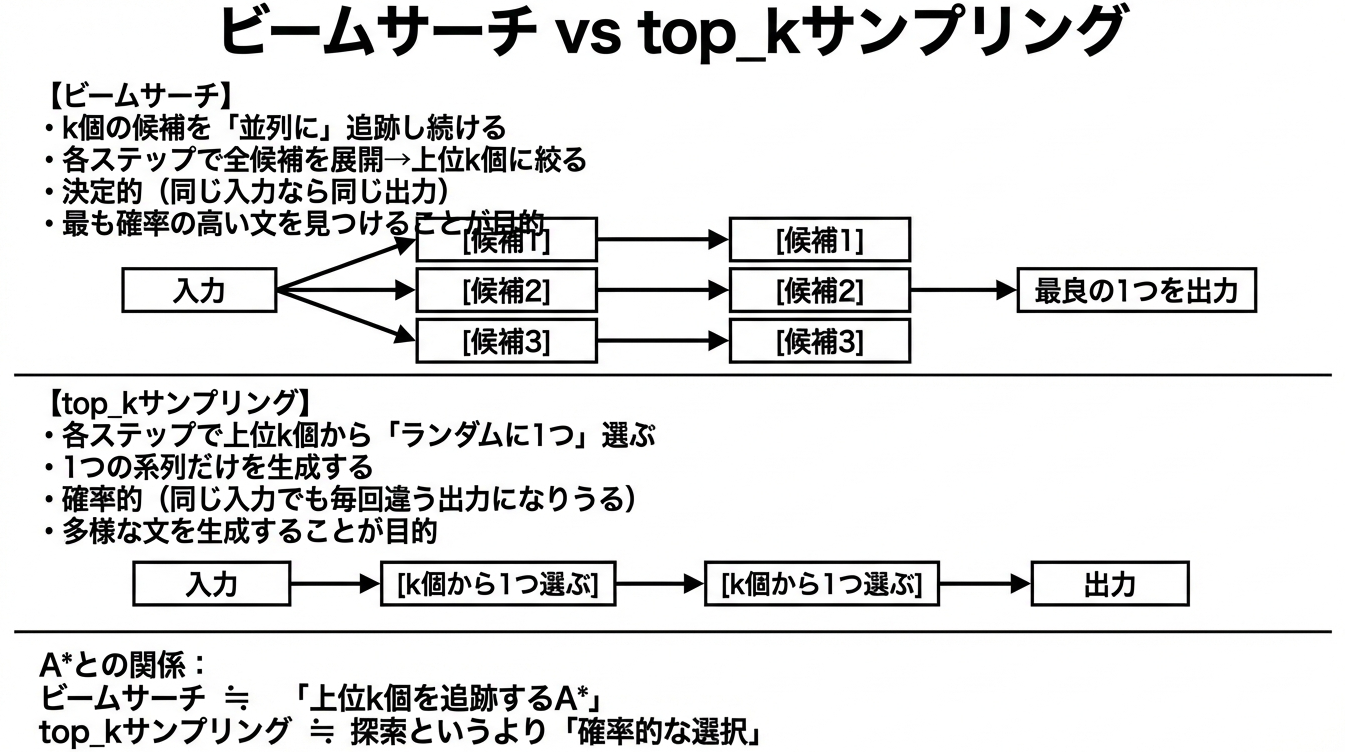
ビームサーチがAと似ているのは、「最も良さそうな候補を優先的に探索する」という点です。Aは最も良い1つを追跡しますが、ビームサーチはk個を並列に追跡することで、「最初の選択が悪くても途中で挽回できる」という柔軟性を持たせています。

【ご参考】Top-Kについては以下 LLMサンプリング解説記事でも触れています

5. AlphaGo：探索と深層学習の融合

囲碁AI「AlphaGo」は、探索ベースと学習ベースの融合という点で画期的でした。

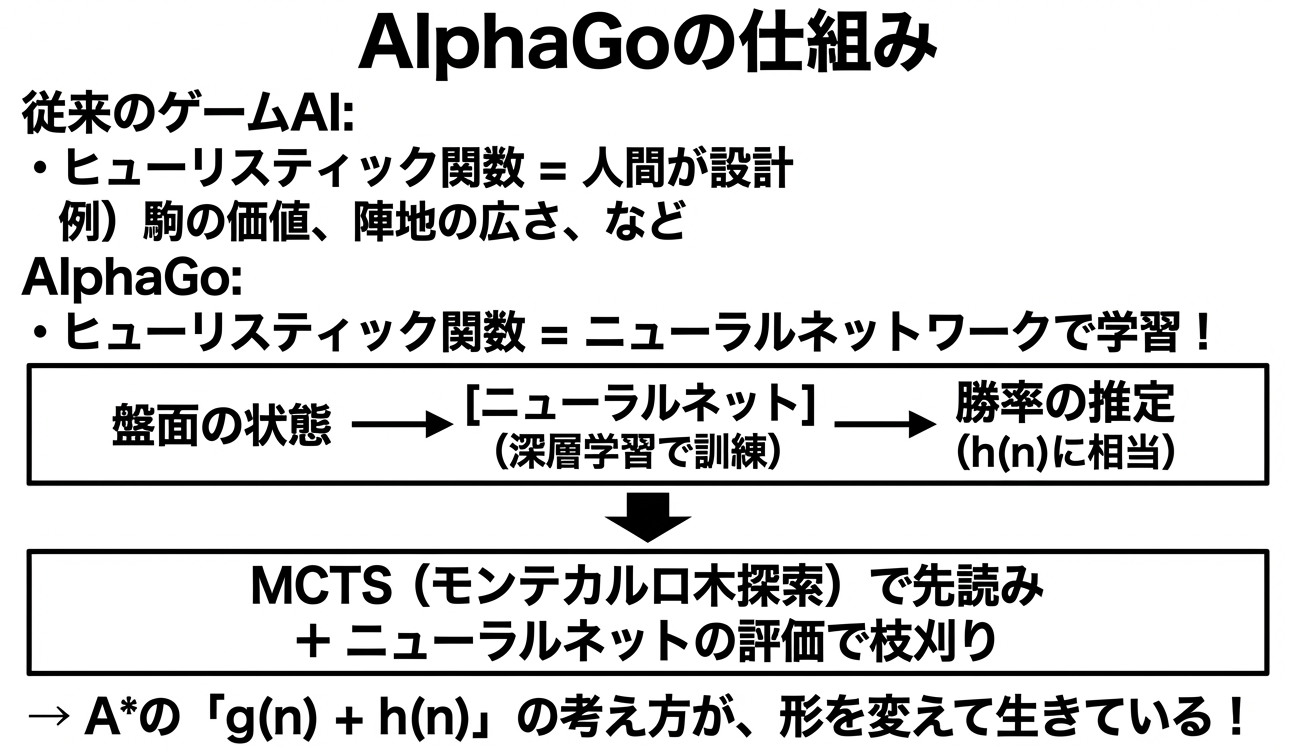
15パズルでは、マンハッタン距離という「人間が設計したヒューリスティック」を使いました。しかし囲碁のような複雑なゲームでは、良いヒューリスティック関数を人間が設計するのは非常に難しいです。

AlphaGoの革新は、このヒューリスティック関数をニューラルネットワークで自動的に学習したことです。大量の棋譜データと自己対戦から、「この盤面はどちらが有利か」を判断する能力を獲得しました。

つまり、「探索」の枠組みはそのままに、「賢い推定」の部分を深層学習で置き換えたのがAlphaGoなんです。

ディープラーニングやランダムフォレストとの関係は？

「ディープラーニング」や「ランダムフォレスト」は、主に学習ベースのAI技術です。

分類	探索ベース（今回の話）	学習ベース
考え方	問題の構造が明確（状態、行動、ゴールが定義できる）	データから「パターン」を学ぶ
目的	「正解への道筋」を探す	明示的なゴールがないことも
代表例	パズル、経路探索、ゲームAI	画像認識、音声認識、推薦システム
代表的な手法	A*探索、ゲーム木探索、制約充足	ディープラーニング、ランダムフォレスト

両者は「競合」ではなく「補完」の関係です。AlphaGoのように組み合わせると、それぞれの強みを活かした強力なシステムが作れます。

まとめ：シンプルなパズルが教えてくれること

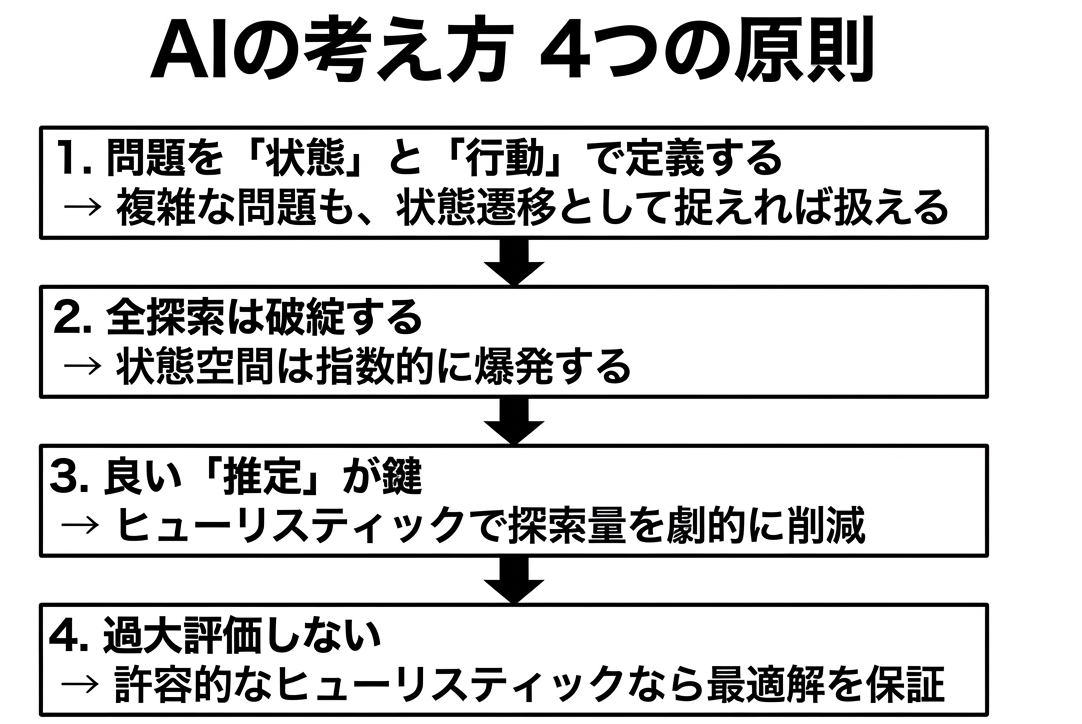
AIは魔法ではありません。「状態をどう定義するか」「どう推定するか」という地道な工夫の積み重ねです。

そして、この基本的な考え方は1960年代から変わっていません。最新のAIも、こうした古典的な知恵の上に成り立っているんです。

実際にAIが解く様子を見てみよう

最後に、ここまで説明したアルゴリズムが実際に動く様子を見てください。

「SHUFFLE」でパズルを崩して、「AUTO SOLVE」を押すと、AIが1手ずつ解いていきます。

統計情報の見方

項目	説明
現在の深さ上限	IDA*が試している閾値。解が見つからないと徐々に増える
探索ノード数	実際に調べた状態の数。難易度が上がると指数的に増加
解の手数	見つかった解の長さ。これが最短経路
探索時間	計算にかかった時間（ミリ秒）。難易度で劇的に変わる

難易度を変えると、これらの数値が劇的に変わることがわかるはずです。

難易度別の探索量（目安）

難易度	シャッフル	探索ノード	探索時間
Easy	15手	数千	数ミリ秒
Normal	30手	数万	数十ミリ秒
Hard	50手	数十万	数百ミリ秒
Expert	80手	数百万	数秒

難易度が上がると探索量が指数的に増えていくのがわかります。

これが「計算量の爆発」を体感できる瞬間です。

コード解説：IDA*探索の実装

興味のある人向けに、実際のコードを解説します。このゲームで使っているのは「IDA*（反復深化A*）」というアルゴリズムです。通常のA*より省メモリで、15パズルのような問題に向いています。

IDA*とは何か？

IDAは「Iterative Deepening A」の略で、日本語では「反復深化A*」と呼びます。

通常のAには一つ弱点があります。それはメモリ消費です。Aは「まだ調べていない候補」をすべてメモリに保持する必要があります。15パズルのような巨大な状態空間では、メモリが足りなくなることがあります。

IDA*はこの問題を解決するために、深さ制限付きの探索を繰り返すという戦略を取ります。

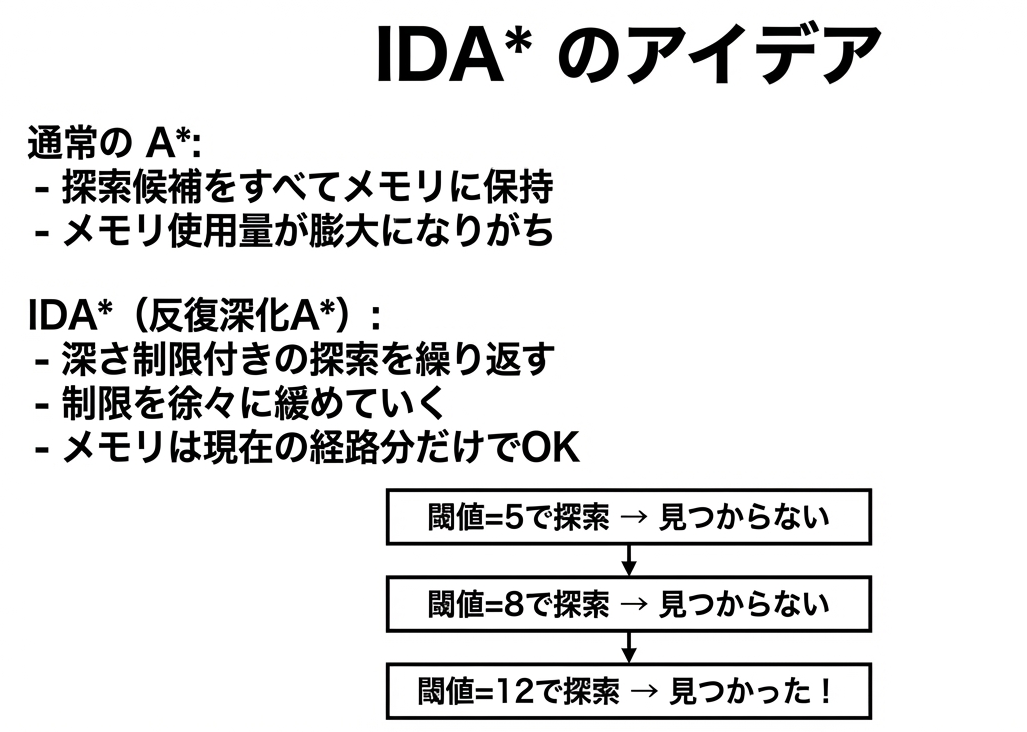
なぜこれがうまく機能するのか？

「同じところを何度も探索するのは無駄では？」と思うかもしれません。確かに無駄はあります。しかし、状態空間は指数的に増えるので、最後の反復が全体の計算時間のほとんどを占めます。

たとえば、閾値10で解が見つかるとしましょう。閾値5、6、7、8、9での探索は、閾値10での探索に比べて、合計しても数%程度に過ぎません。なぜなら、探索量は閾値が大きくなるほど指数的に増えるからです。

つまり、「少しの無駄」と引き換えに、「メモリをほとんど使わない」という大きなメリットを得ているのです。

マンハッタン距離（ヒューリスティック関数）

function manhattanDistance(state) {
  let distance = 0;
  for (let i = 0; i < state.length; i++) {
    const tile = state[i];
    if (tile !== 0) {
      // ゴール位置を計算
      const goalRow = Math.floor(tile / 4);
      const goalCol = tile % 4;
      // 現在位置を計算
      const currentRow = Math.floor(i / 4);
      const currentCol = i % 4;
      // 縦横の距離を足す
      distance += Math.abs(goalRow - currentRow) 
               + Math.abs(goalCol - currentCol);
    }
  }
  return distance;
}

各タイルについて「あるべき場所」と「今いる場所」の縦横の差を計算し、全部足し合わせます。空欄（0）は無視します。

このコードのポイントは、タイルの「値」からゴール位置を計算しているところです。たとえばタイル5は、ゴール状態ではインデックス5（2行目の2列目）にあるべきです。5 / 4 = 1（行）、5 % 4 = 1（列）で計算できます。

IDA*のメインループ

function idaStar(startState) {
  let threshold = manhattanDistance(startState); // 初期閾値
  const path = [startState];

  while (true) {
    const result = search(path, 0, threshold);
    
    if (result === 'FOUND') {
      return path; // 解が見つかった
    }
    
    if (result === Infinity) {
      return null; // 解なし
    }
    
    threshold = result; // 閾値を上げて再探索
  }
}

IDA*は「深さ制限付き深さ優先探索」を繰り返します。最初はマンハッタン距離を閾値にして探索し、見つからなければ閾値を上げて再挑戦します。

ここで重要なのは、閾値の更新方法です。search 関数は、閾値を超えた中で最小の f(n) 値を返します。これが次の閾値になります。こうすることで、「ギリギリで諦めた候補」を次の反復で調べることができます。

再帰的な探索

function search(path, g, threshold) {
  const current = path[path.length - 1];
  const f = g + manhattanDistance(current);

  // 閾値を超えたら打ち切り
  if (f > threshold) {
    return f;
  }

  // ゴール判定
  if (isGoal(current)) {
    return 'FOUND';
  }

  let min = Infinity;
  
  // 隣接状態を探索
  for (const neighbor of getNeighbors(current)) {
    path.push(neighbor);
    const result = search(path, g + 1, threshold);
    
    if (result === 'FOUND') {
      return 'FOUND';
    }
    
    if (result < min) {
      min = result;
    }
    
    path.pop(); // バックトラック
  }

  return min;
}

f = g + h が閾値を超えたら、その枝の探索を打ち切ります。これにより、ゴールから遠そうな状態を効率的に枝刈りできます。

path.pop() の部分は「バックトラック」と呼ばれる操作です。「この方向はダメだった」ときに、一歩戻って別の方向を試します。これがIDA*がメモリを節約できる理由です。探索候補をすべて保持するのではなく、「今いる経路」だけを保持すればいいです。

おまけ：3×3＋1 絵合わせパズルも解いてみよう！

さて、ここまで読んでくれた人へのおまけです。

スライドパズルには、もう一つよく見る形がありますよね。上に1マスの空欄があって、下に3×3の絵が配置されているタイプ。お土産屋さんとかでよく見かけるあれです。

たいてい子供用にディズニーなどのかわいいキャラクターが描かれています。

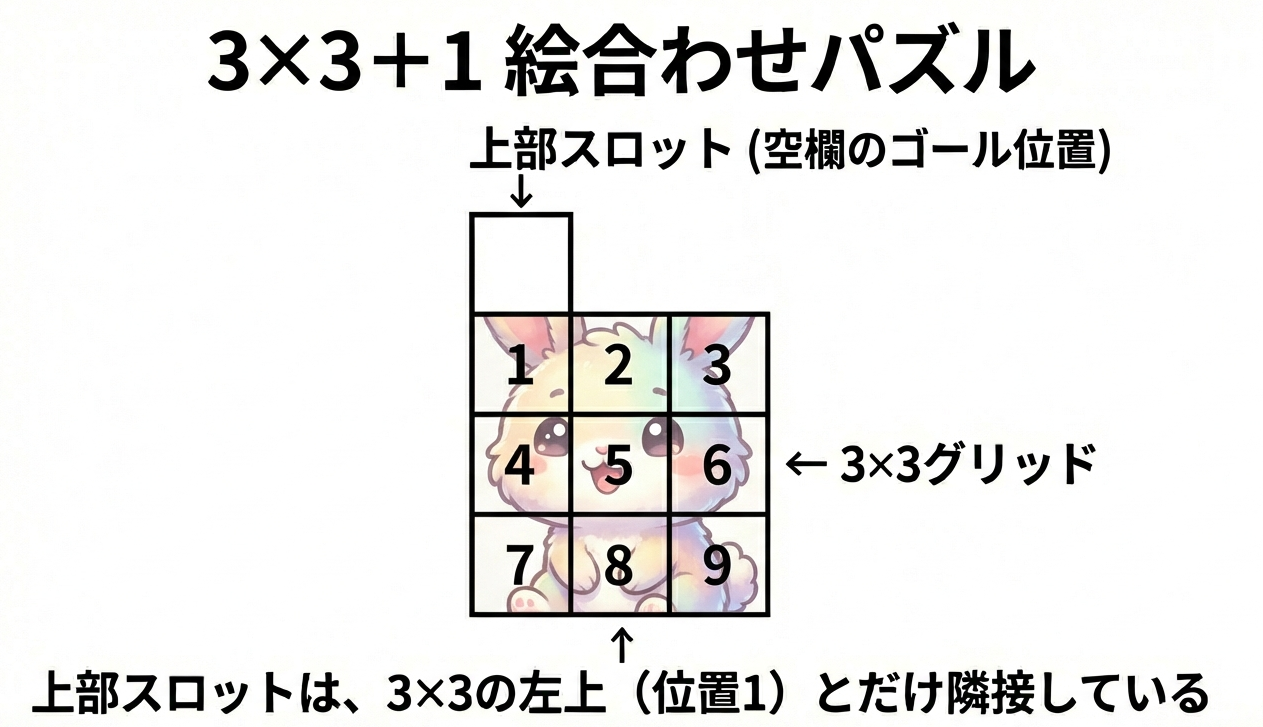
解法は同じ？

はい、基本的に同じIDA*探索で解けます！

違いは「隣接関係」の定義だけです。

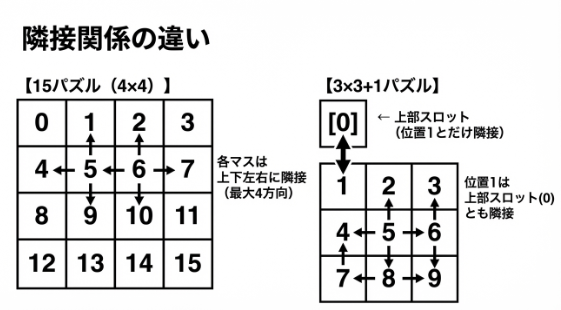
計算量の違い

状態数の比較

パズル	マス数	状態数（概算）
3×3＋1	10マス	10!/2 ≒ 180万通り
15パズル	16マス	16!/2 ≒ 10兆通り

3×3＋1は15パズルの約500万分の1！だから探索が圧倒的に速いんです。

3×3＋1パズルは状態数が少ないので、AIの探索がとても速く終わります。「計算量の違い」を体感するのにぴったりですね。

実際に遊んでみよう

こちらも同じくIDA*探索を実装したバージョンを作りました。

15パズルと比べて、探索ノード数や探索時間がどれくらい違うか、ぜひ比較してみてください！

コードの違い

アルゴリズムはほぼ同じで、隣接関係の定義だけが違います。

// 3×3＋1パズルの隣接関係
function getAdjacentIndices(index) {
  const adjacency = {
    0: [1],           // 上部スロット → 左上(1)のみ
    1: [0, 2, 4],     // 左上 → 上部スロット, 右, 下
    2: [1, 3, 5],
    3: [2, 6],
    4: [1, 5, 7],
    5: [2, 4, 6, 8],  // 中央 → 上下左右
    6: [3, 5, 9],
    7: [4, 8],
    8: [5, 7, 9],
    9: [6, 8]
  };
  return adjacency[index] || [];
}

15パズルでは「上下左右」を計算で求めていましたが、3×3＋1パズルでは上部スロットという特殊な位置があるので、隣接関係をテーブルで定義しています。

この「問題の構造に合わせて隣接関係を定義する」というのも、状態空間探索の重要なポイントです。問題が変わっても、アルゴリズムの骨格は同じ。変わるのは「状態の表現」と「隣接関係」だけです。

おわりに

15パズルという素朴なおもちゃが、AI研究の原点であり、現代の技術にもつながっているというお話でした。

「考える」とは何か。この問いに対する一つの答えが「状態空間を探索すること」です。そして、賢く探索するための工夫が、ヒューリスティックというアイデアでした。

次に15パズルや絵合わせパズルを見かけたら、ぜひAIの気持ちになって解いてみてください。

「今の状態からゴールまで、最低何手かかるか？」と考えながら。

それが、AIの「考え方」を体験する第一歩となるとおもいます。

それでは、今回もお読みいただきありがとうございました。

また次回お会いしましょう！

以下の記事も今回と同様、ゲームを題材にAI基礎理論「情報理論」を解説しています。